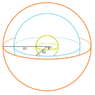
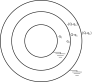
The self-capacitance of an isolated sphere is defined as 4πε₀R, but the discussion reveals confusion regarding its application when multiple spheres are involved. Participants suggest treating the setup as two parallel capacitors formed by the spheres, emphasizing the need to calculate electric fields and potentials between them. The potential differences must be equated to determine the charge distribution on the spheres, and Gauss's Law is recommended for calculations. Ultimately, the self-capacitance is found to equal the parallel combination of the capacitors, leading to a final value derived from the charge and potential differences. The conversation highlights the complexities of capacitance calculations in multi-sphere systems.