Calculating Tension & Buoyancy in Water

  • Context: High School 
  • Thread starter Thread starter Boxlife27
  • Start date Start date
  • Tags Tags
    Buoyancy Tension
Click For Summary
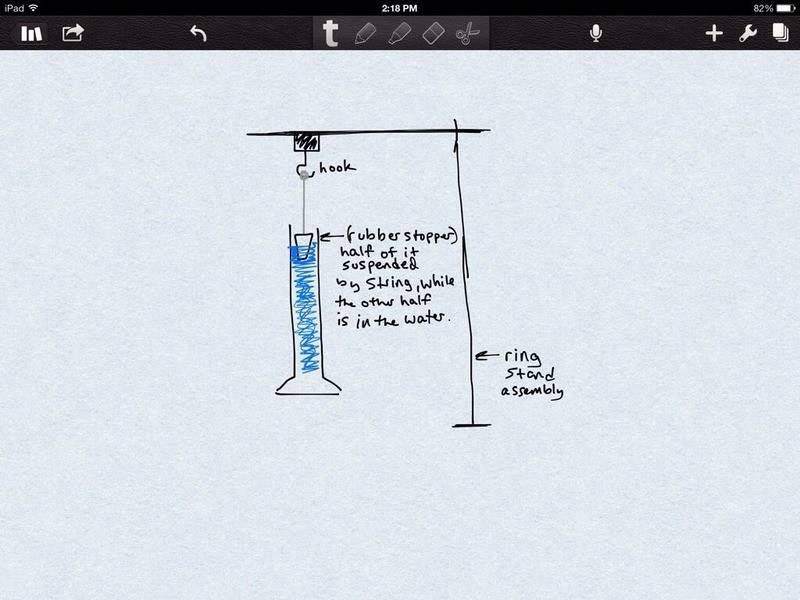
SUMMARY

This discussion focuses on calculating the tension in a string suspending a rubber stopper that is half-submerged in water. The key concepts include buoyant force, which is calculated using the formula ρ x V x g, where ρ is the density of water (1000 kg/m³), V is the displaced volume, and g is the acceleration due to gravity. The tension in the string (T) can be determined using the equation T = W - F_b, where W is the weight of the stopper and F_b is the buoyant force. The discussion emphasizes the importance of understanding Archimedes' Principle in determining the buoyant force when only part of the object is submerged.

PREREQUISITES
  • Understanding of Archimedes' Principle
  • Knowledge of buoyant force calculations
  • Familiarity with free body diagrams (FBDs)
  • Basic physics concepts related to weight and density
NEXT STEPS
  • Study the application of Archimedes' Principle in various scenarios
  • Learn how to calculate buoyant force for partially submerged objects
  • Explore advanced free body diagram techniques for complex systems
  • Investigate the effects of different densities on buoyancy calculations
USEFUL FOR

Students in AP Physics, educators teaching buoyancy concepts, and anyone interested in understanding the principles of tension and buoyancy in fluid mechanics.

Boxlife27
Messages
12
Reaction score
0
Hello, if I were to suspend a rubber stopper into a graduated cylinder filled with water, with the stopper half in the h2o and half out of it, how would i calculate the tension in the string? Experimentally, i would collect the displaced volume, density (1000kg/m3), and mass of stopper. I am only in AP physics B, so i cannot use an extremely intense formula. I know buoyant force is rho x volume x gravity and weight is mass x gravity obviously. Any help on this soon would be great. Thank you!
ImageUploadedByPhysics Forums1385065647.393557.jpg
 
Physics news on Phys.org
What forces are acting on the rubber stopper? What is causing the tension in the string in the first place?
 
Have you been taught to use free body diagrams? If so, you should have no trouble answering SteamKing's question.
 
Yes I know how to use fbds, however only half of the rubber stopper is in the water. It is not submerged. For the submerged experiment, I would do T equals W minus Force buoyancy. But when only half of the stopper is in the water (and it is not floating, it's being suspended by the string), how would this equation change? Thank you
 
Archimedes Principle
 
Boxlife27 said:
Yes I know how to use fbds, however only half of the rubber stopper is in the water. It is not submerged. For the submerged experiment, I would do T equals W minus Force buoyancy. But when only half of the stopper is in the water (and it is not floating, it's being suspended by the string), how would this equation change? Thank you
If it's only half-submerged, that only affects the magnitude of the buoyant force on the stopper. It doesn't affect qualitatively the free body diagram or the identification of the forces acting on the stopper.
 
Thank you very much for answering. How would the magnitude be affected? Would the buoyant force be in half? Or something of that nature.. Thanks
 
Boxlife27 said:
Thank you very much for answering. How would the magnitude be affected? Would the buoyant force be in half? Or something of that nature.. Thanks
Can you articulate Archimedes Principle? If you can state the principle, you should have no trouble determining the buoyant force.
 
Oh yes, I was overthinking it. Thank you all for the help
 

Similar threads

High School Does Buoyancy Apply When Not Fully Submerged?
  • · Replies 7 ·
Replies
7
Views
2K
High School Fully submerged block in a pool of water
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad What is the location of the center of buoyancy and how is it determined?
  • · Replies 14 ·
Replies
14
Views
10K
High School What is my apparent weight in water?
  • · Replies 14 ·
Replies
14
Views
3K
Undergrad What are the effects of Buoyancy & G-force combined in this scenario?
  • · Replies 9 ·
Replies
9
Views
2K
High School Water Wicking between two containers
  • · Replies 2 ·
Replies
2
Views
639
High School What happens to buoyancy when a non-uniform force is applied to the liquid?
  • · Replies 5 ·
Replies
5
Views
2K
Volume's effect on buoyancy: Does pressure increase?
  • · Replies 11 ·
Replies
11
Views
2K
High School Archimedes Principle - A Rock and Water Magic Trick
  • · Replies 29 ·
Replies
29
Views
3K
High School Archimedes principle and the density of a rock
  • · Replies 6 ·
Replies
6
Views
6K