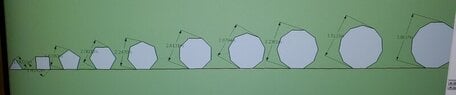
Discussion Overview
The discussion revolves around calculating the maximum diameter of regular polygons with a side length of one, exploring whether this can be done without using pi or any nonterminating numbers. Participants examine various mathematical approaches and implications related to the properties of regular polygons and their diameters.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant presents measured maximum diameters for regular polygons with side lengths of one and seeks a general formula for any number of sides without using pi.
- Another participant suggests deriving a formula based on inscribing polygons in circles and using trigonometric functions to find the radius.
- Some participants question whether the diameters of these polygons are algebraic numbers or transcendental, expressing skepticism about the possibility of a constructive proof.
- There is a discussion about the feasibility of creating a regular polygon with sides of a planck length and its implications for visibility and measurement.
- Participants debate the nature of exact measurement and representation in mathematics, particularly regarding irrational numbers and their decimal expansions.
- Some express that polygons with straight edges do not necessarily provide a means to approximate pi with terminating decimal expansions.
- There are off-topic discussions about base representations of numbers, particularly in relation to pi and the digits used in base pi.
Areas of Agreement / Disagreement
Participants express multiple competing views regarding the calculation of diameters, the nature of numbers involved, and the implications of using straight lines versus curves. The discussion remains unresolved with no consensus on the feasibility of the proposed methods or the properties of the diameters.
Contextual Notes
Participants note limitations regarding the assumptions made about the nature of numbers and measurements, as well as the scope of the discussion concerning practical applications versus theoretical constructs.