Calculating the magnetic field in this seemingly simple case?

[Abdullah Almosalami]

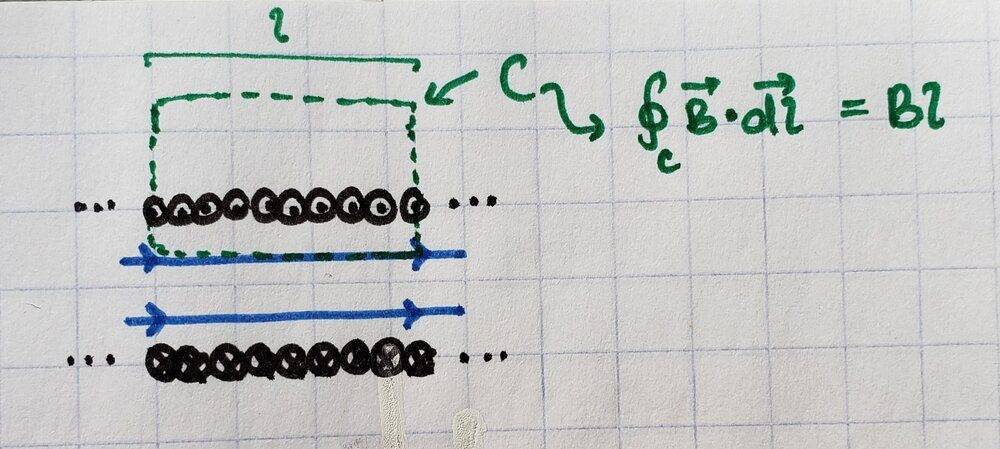
A classic example in textbooks is calculating the magnetic field inside a solenoid of length $l$ with $N$ turns and making the assumption that the magnetic field inside the solenoid is pretty uniform and outside it is 0. Using Ampere's law $\oint_C \vec B \cdot d \vec l = \mu_0 I_{through}$ , if you do the line integral of $\vec B \cdot d \vec l$ over a well-chosen path with the assumptions in mind, you get $B = \mu_0 \frac N l I$.

Now my question begins with placing a "core" material. Specifically,

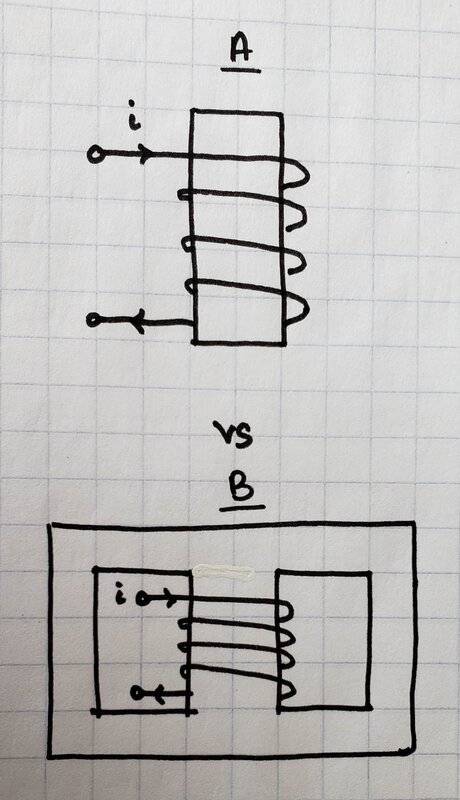
Both are wound the same way, same current, # turns, and same core material. Also, say the cross-sectional area of the winding is the same in both cases. The first case 'A' is still a common example. If the core material has a magnetic relative permeability of $\mu_r$ (ignore the madness of hysteresis), then we just multiply that in with what was derived earlier, namely that now $B = \mu_r \mu_0 \frac N l I$.

But in the second case 'B', I'm getting a little uneasy... I might naively do the same path of $\vec B \cdot \vec dl$ as shown in the first pic and use the same assumptions and conclude that the magnetic field is the same but I know that would be wrong. I might do a path like this:

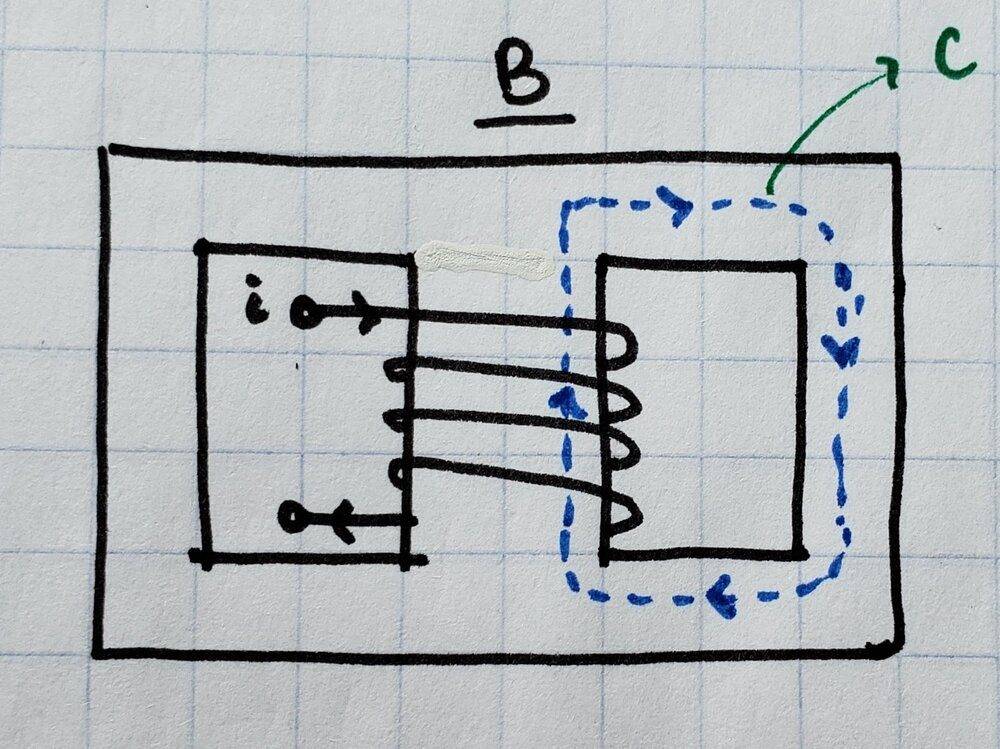
and assume that the magnetic field is constant along the path, but that doesn't feel right either, and also would lead me to believe the magnetic field is less because $\oint_C \vec B \cdot d \vec l$ is larger with the same current and longer path so $B$ must be smaller. So I'm not sure how I'd tackle this...

Qualitatively, I know that B will have a stronger magnetic field inside the coil because I know that B has a higher inductance just from looking at inductors I have lying around in the school lab. If A and B have the same cross-sectional area, and you experimentally observe that $L_A < L_B$, let's say by some factor $\alpha$, then the magnetic field in the winding will also differ by the same factor since inductance is the amount of flux for a given current and they have the same cross-sectional area, and since the magnetic field in A is easier to calculate, I might use that to approximate what B's magnetic field would be.

I might hypothesize to explain why B has a stronger magnetic field by imagining each "section" of the frame that makes up B's core as contributing its own magnetic field to the inner part of the winding once it is magnetized, and then just superposition. B has more "frame" contributing magnetic field than A so yeah. Would that be the right idea?

 

[hutchphd]

This wikipedia article is pretty good:

https://en.wikipedia.org/wiki/Maxwell's_equations#Bound_charge_and_current

Also Griffiths does a good job with electrodynamics in media. In particular you need to understand the use of bound currents to describe a material with magnetization M caused by dipolar alignment. These contribute to B but only the free (and displacement) currents appear in Maxwells equation for H. I am not certain you understand the basics.

 

[rude man]

Magnetic circuits are similar to electric.
The governing equation for magnetic circuits is
mmf = Ni = flux x reluctance
where mmf = magnetomotive force, analogous to emf for electric circuits.
N = number of turns in coil, i = current.

And reluctance = $length~ of~ path/(\mu \cdot cross-sectional~ area)$.
Quite analogous to electric circuits, again.

Your "B" illustrates further the fact that magnetic circuits can have parallel paths, just like in electrical. The left leg is in parallel with the right leg.

So show another dashed path in the left side which obviously runs counter to the right-hand path. The flux in the middle section (where the coil windings are located) will thus have double the flux in either the left or right sections.

Inductance = N times flux/i = $N^2/reluctance$
where reluctance is half the reluctance of either the left or right path.

You have doubled the inductance with the B configuration over what it would be with just one leg.

 

[hutchphd]

Sometimes examination of mgnetic circuits is useful. I do not think this is one of them.
The OP is trying to compare the solution for a short solenoid to to that of an H core, not the effect of different "legs" of the H core.

Also the analysis is incorrect:

You have doubled the inductance with the B configuration over what it would be with just one leg.

This is strictly true only in the limit that each leg Reluctance is large compared to that of the magnet "core'. If instead they are equal the gain will be a factor of $\frac 3 2$ . If instead the "core"has a high reluctance it buys you ~ nothing.

But unless the short solenoid can be characterized as being in a magnetic circuit I do not see why this addresses the initial question.

Again the issue for the OP is to understand that the line integrals using free currents should contain H and not B..