The forum discussion focuses on calculating the radius R of a circle given points A, B, C, and D with specific distances and ratios. The initial calculations led to an incorrect conclusion of R = 250√2, which was later corrected to R = 312.5 after addressing the geometric constraints of the points. The final correct solution was derived using the cosine rule and proper assumptions about the order of points on the circle, leading to R = 1250/3 under certain conditions.
PREREQUISITESMathematicians, geometry enthusiasts, students studying trigonometry, and anyone interested in solving geometric problems involving circles and triangles.
anemone said:
Did anyone notice that that solution cannot possibly be correct? If $x=5$ (in the unknown units) then AD = AC, which is geometrically impossible, because AD is obviously shorter than AC. What I did wrong was that the calculation for $R$ is correct, giving $R=5/\sqrt2$ (in the unknown units), but when you substitute that value to get an equation for $x$, the equation does not reduce to $(x^2-25)^2 = 0$, but to $(x^2-18)(x^2-32) = 0$. Thus $x=3\sqrt2$ or $4\sqrt2$. But $3\sqrt2<5$, which would mean that AC < AD. That can't happen if the points A, B, C, D occur in that order on the circle. Therefore $x=4\sqrt2$ in unknown units, and the scaling factor to convert unknown units to standard units is $500/(4\sqrt2).$ So the correct solution is $R = \dfrac5{\sqrt2}\,*\,\dfrac{500}{4\sqrt2} = \boxed{312.5}.$Opalg said:
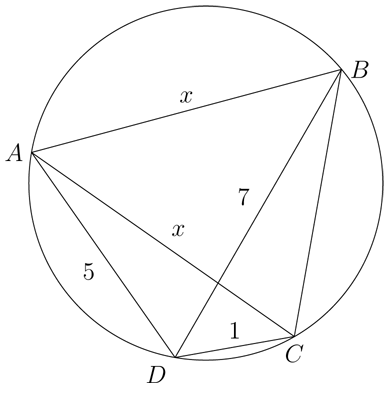
Suppose that the distances DC, DA, DB are respectively 1, 5, 7, in some unknown units. Then AC and AB (which are known to be 500 in standard units) will be equal to $x$, say, in the unknown units.
The circle is the circumcircle of the triangles ABD and ACD. The circumradius of a triangle is always equal to one half of a side of the triangle divided by the sine of the opposite angle. Thus in the triangle ABD, $\sin(\angle BAD) = \dfrac7{2R}$; and in the triangle ACD, $\sin(\angle ADC) = \dfrac x{2R}.$
The cosine rule in triangle ABD gives $\cos(\angle BAD) = \dfrac{x^2-24}{10x}$; and in triangle ACD it gives $\cos(\angle ADC) = \dfrac{26-x^2}{10}.$
Now use $\sin^2 + \cos^2 = 1$ for those two angles to get the equations $$\frac{49}{4R^2} + \frac{(x^2-24)^2}{100x^2} = 1, \qquad \frac{x^2}{4R^2} + \frac{(26-x^2)^2}{100} = 1.$$ Multiply out the fractions to get $$25*49x^2 + R^2(x^2-24)^2 = 100R^2x^2, \qquad 25x^2 + R^2(26-x^2)^2 = 100R^2.$$ Subtract the second equation from the first to get $-96R^2x^2 + 25*48x^2 = 0$, which leads to $R = 5/\sqrt2$ (in the unknown units). Substitute that value for $R$ into one of the two equations, which then reduces to $(x^2-25)^2 = 0$. Thus $x=5$. But we know that $x=500$ in standard units, so we need to multiply by 100, giving $\boxed{R= 250\sqrt2}$ as the solution.
Opalg said:
You certainly have not messed up on the problem. I think that the question of whether the points come in the order ABCD or ABDC as you go round the circle is absolutely critical. If they come in the order ABDC then that would correspond (in my solution) to the case where $x^2 = 18$, in which case I agree with your answer $R=1250/3$. I assumed that the order would be ABCD, in which case $x^2 = 32$ and $R = 1250/4$.anemone said:
