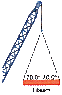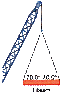SUMMARY
The tension in each cable supporting a steel I-beam weighing 8.90 kN, lifted at a constant velocity, can be calculated using equilibrium equations. The weight in Newtons is 8900 N. The relationship between the tension (T) in the cables and the weight (W) is established through the equation 2Tsin(70°) = W. Solving this yields T = W / (2sin(70°)), resulting in a tension of approximately 4735.59 N in each cable.
PREREQUISITES
- Understanding of static equilibrium in physics
- Knowledge of trigonometric functions, specifically sine and cosine
- Ability to convert units from kilonewtons to newtons
- Familiarity with free body diagrams (FBD)
NEXT STEPS
- Study the principles of static equilibrium in mechanics
- Learn how to apply trigonometric functions in physics problems
- Practice converting between different units of force and weight
- Explore advanced applications of free body diagrams in engineering contexts
USEFUL FOR
Students in physics or engineering, structural engineers, and anyone involved in the analysis of forces in static systems will benefit from this discussion.