Calculating Total Weight of 10 Oscillators & 8 Quanta of Energy

[SidMe1984]

1. The problem statement

Consider the case of 10 oscillators and eight quanta of energy. Determine the dominant configuration of energy for this system by identifying energy configurations and calculating the corresponding weights. What is the probability of observing the dominant configuration?

Attempt at the solution:

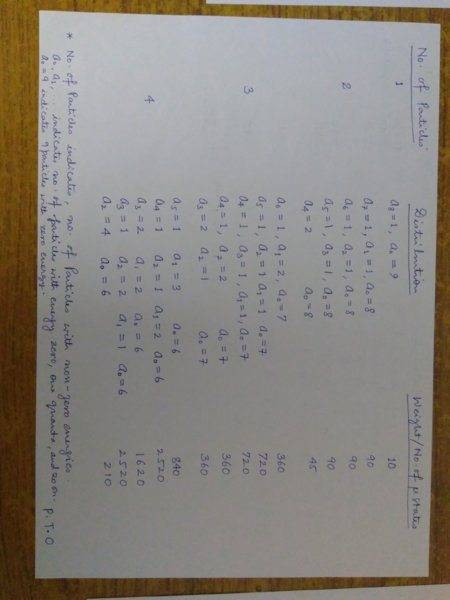
To add to the information on the problem, I picked it from Engel and Reed (Thermodynamics, Statistical thermodynamics,...) Chapter 13.

I checked the answer to the problem in the book, it says that the probability for the most probable state is 0.25 but the book gives no details of the working.

What I found was that the desired probability is less than 0.25. Clearly then there is some limitation imposed on the energy levels available to the oscillators. I simply cannot guess this particular limitation.

If I should be getting a probability of 0.25 for the most probable configuration, I must have the sum total of all the weights equal to about 20,170 ... I am unable to come to this count and I need help with this part of the problem.Can you please guide me with it. Thanks

 

[mfb]

The first picture is rotated.

Did the book specify harmonic oscillators? Assuming yes:

Some checks:
There are 22 partitions of 8, so you should have 22 cases - good.
Checked several multiplicities and they are right as well, including the 5040.
Either the book answered a different question or 1/4 is wrong.

 

[TSny]

Check the 1620 value. Shouldn't that be 1260? This will reduce your total number of states to 24310, which agrees with another way of calculating the total number as 17!/(9! 8!)

Unfortunately, this still doesn't yield 0.25 for the probability of getting the 5040-configuration.