Calculating Triangle Side Length with Known Angles and Radius

In summary, the formula for finding the length of a triangle's side depends on the type of triangle. You can use the Pythagorean theorem for a right triangle, divide the perimeter by 3 for an equilateral triangle, and use the law of cosines or law of sines for a scalene or isosceles triangle. You need at least one side length to find the length of a triangle's side, and knowing all three angles does not provide enough information. To find the length of a triangle's side, you need to know the length of at least two other sides or one side and an opposite angle. The length of a triangle's side cannot be negative, and it is typically measured using the same units as the
  • #1
BrentK
21
0
Hi there.
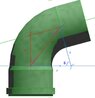
Can someone tell me how to calculate the length of "a", shown in these drawings?
"r" is the radius of the corner, so these 2 sides have the same length.
"C" is 90 deg
angle "B" is known (the angle of the corner)

Here are the diagrams. First example 45 degree corner, second example 75 deg corner.

Many thanks in advance for your help! (Nerd) ;)

View attachment 8683

View attachment 8684
 

Attachments

  • piep45m.jpg
    piep45m.jpg
    25.1 KB · Views: 63
  • pipe75m.jpg
    pipe75m.jpg
    28.6 KB · Views: 60
Mathematics news on Phys.org
  • #2
If I understand the problem correctly, the answer is $a = r\tan\bigl(\frac12B\bigr)$.
 
  • #3
Thanks Opalg!
That works perfectly!
So easy... I was trying to hard (Dull)
 

Related to Calculating Triangle Side Length with Known Angles and Radius

1. What is the formula for finding the length of a triangle's side?

The formula for finding the length of a triangle's side depends on the type of triangle. For a right triangle, you can use the Pythagorean theorem (a² + b² = c²) to find the length of the hypotenuse. For an equilateral triangle, all three sides are equal, so you can divide the perimeter by 3 to find the length of each side. For a scalene or isosceles triangle, you can use the law of cosines or the law of sines to find the length of a side.

2. Can I find the length of a triangle's side if I only know the angles?

No, you need at least one side length to find the length of a triangle's side. If you know all three angles of a triangle, you can use the law of sines or the law of cosines to find the length of a side, but you would still need to know the length of at least one other side.

3. How many sides of a triangle do I need to know to find the length of the remaining side?

To find the length of a triangle's side, you need to know the length of at least two other sides or the length of one side and an angle opposite to it. If you know all three sides, you can use the law of cosines to find the length of the remaining side. If you know two sides and the angle between them, you can use the law of sines to find the length of the remaining side.

4. Can the length of a triangle's side be negative?

No, the length of a triangle's side cannot be negative. Length is a physical measurement and cannot have a negative value. If you get a negative answer when solving for the length of a triangle's side, it means that there was an error in your calculations.

5. What units are used to measure the length of a triangle's side?

The length of a triangle's side is typically measured using the same units as the other sides and angles of the triangle. Common units include centimeters, inches, and degrees. It is important to use consistent units when solving for the length of a triangle's side.

Similar threads

MHB Find Length of Side in Right Triangle w/ 45°, 90°, and 45° Angle
    • General Math
Replies
2
Views
1K
Triangle Math Help: Calculate Angles & Lengths with 46 & 35 Measurements
    • Precalculus Mathematics Homework Help
Replies
11
Views
1K
MHB Angle calculation in a sloping vector system
    • General Math
Replies
1
Views
1K
MHB What is the smallest side length BC of triangle ABC with fixed angle and area?
    • General Math
Replies
2
Views
1K
MHB Finding exact 3d coordinates in a falling pipe system with corners
    • General Math
Replies
20
Views
3K
MHB Length of sides of right triangle with 1 angle and 1 side
    • General Math
Replies
2
Views
1K
MHB Question about a rounded rectangle
    • General Math
Replies
1
Views
7K
Area of interior triangle of pyramid normal to a side length
    • Precalculus Mathematics Homework Help
Replies
3
Views
1K
Trig problem involving a triangle's angles and sides
    • Precalculus Mathematics Homework Help
Replies
5
Views
2K
B How Can Trigonometry Calculate Distances in Surveying?
    • General Math
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top