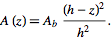Discussion Overview
The discussion revolves around the mathematical derivation of the volume of an arbitrary pyramid, focusing on the relationship between cross-sectional area and height. Participants explore the scaling of areas and dimensions as one moves from the apex to the base of the pyramid, considering both general principles and specific mathematical formulations.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Conceptual clarification
Main Points Raised
- Some participants express a desire for a clearer mathematical explanation of the volume derivation from the article, particularly regarding the scaling of cross-sectional areas with height.
- It is proposed that thinking downwards from the apex may clarify how the width of the pyramid at a given level relates to the height, suggesting that the area at that level is proportional to the square of the distance from the apex.
- Participants discuss the constant of proportionality, denoted as ##k##, and how it relates to the area at the base and the height of the pyramid, leading to the formulation of the area at height ##z## as ##A(z) = A_b \frac{(h-z)^2}{h^2}##.
- There is a question about the use of ##(h-z)^2## in the area formula, especially in the context of arbitrary pyramids, not just square-based ones.
- Some participants explain that for any flat shape, increasing dimensions proportionally results in area increasing by the square of the scaling factor, providing a general mathematical principle behind the area calculations.
- One participant seeks clarification on whether the reasoning is based on established mathematical laws or intuitive understanding.
- It is stated that the principles discussed are standard mathematics involving the definition of area and multiplication, applicable to various shapes, though some caveats about unconventional mathematical concepts are noted.
Areas of Agreement / Disagreement
Participants generally agree on the mathematical principles regarding area scaling, but there remains some uncertainty and debate about the specific application of these principles to arbitrary pyramids, particularly concerning the formulation of the area at different heights.
Contextual Notes
Some limitations are noted regarding the assumptions made about the shapes involved and the specific definitions of terms used in the discussion, which may affect the clarity of the mathematical derivations.
 at the base ([PLAIN]http://mathworld.wolfram.com/images/equations/Pyramid/Inline5.gif) to 0 at the apex (assumed to lie at a height [PLAIN]http://mathworld.wolfram.com/images/equations/Pyramid/Inline6.gif). The area at a height http://mathworld.wolfram.com/images/equations/Pyramid/Inline7.gif above the base is therefore given by"
at the base ([PLAIN]http://mathworld.wolfram.com/images/equations/Pyramid/Inline5.gif) to 0 at the apex (assumed to lie at a height [PLAIN]http://mathworld.wolfram.com/images/equations/Pyramid/Inline6.gif). The area at a height http://mathworld.wolfram.com/images/equations/Pyramid/Inline7.gif above the base is therefore given by"