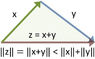
zaddyzad
- 149
- 0
Homework Statement
A trunk of mass m = 1.300 kg is pushed a distance d = 124 cm up an incline with an angle of inclination theta = 28.0 ° by a constant horizontal force P = 425 N (see figure).
The coefficient of kinetic friction between the trunk and the incline is 0.130.
a) Calculate the work done on the trunk by the applied force P.
b) Calculate the work done on the trunk by the frictional force.
c) Calculate the work done on the trunk by the gravitational force.
http://imgur.com/ydGgOn7 http://imgur.com/ydGgOn7
My guess: (P has a component 28degrees above its horizontal, and another one pointing down perpendicular to the plane)
The Attempt at a Solution
A) shouldn't this be W = F*D... (425/cos28)*1.24
b) shouldn't this just be W = FF * D... ((1.3gcos28+425tan28)*.13)*1.24
c)W=Fs*D... 1.3gsin28*1.24
I got all the questions wrong... can anyone tell me where I went wrong ?