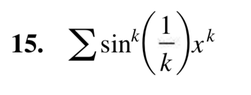yeny
- 7
- 0
Hi guys!
Here's a problem i was working on. I solved it by root test and got absolute value of x on the outside of the limit and the limit equaled zero. Is it wrong to multiply the outside absolute value by the zero I got from the limit? or is that okay?
In general, when we are solving power series problems, is it okay to think of R equals infinity when the limit is zero? is that always the case? the interval of convergence is (-inf, +inf)
what are the steps that YOU would take to solve such a problem?
hope this makes sense. THANK YOU !
View attachment 8520
View attachment 8519
Here's a problem i was working on. I solved it by root test and got absolute value of x on the outside of the limit and the limit equaled zero. Is it wrong to multiply the outside absolute value by the zero I got from the limit? or is that okay?
In general, when we are solving power series problems, is it okay to think of R equals infinity when the limit is zero? is that always the case? the interval of convergence is (-inf, +inf)
what are the steps that YOU would take to solve such a problem?
hope this makes sense. THANK YOU !
View attachment 8520
View attachment 8519