Can an Ellipse Help Solve the Scalene Triangle Problem?

[Samwise-zambeezi]

Hi guys!

I've got a problem with a triangle, and I'm frazzled my brain trying to work it out (not even sure if what I'm looking for is possible with the info I have!).

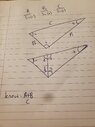
Pic of the offending triangle attached.

Basically, I know the length of C and the sum of lengths A and B.

Now, if C was static and remained unchanged, but if the point c was to move, lengths A and B would change. I'm trying to find the individual lengths of A and B at the point at which, C is split with a vertical into two equal angles (f and g).

Is this possible? Hope this is clear enough, any tips would be a massive help.

Best regards

Swise

 

[Opalg]

If the point $c$ moves so that the sum of its lengths to $a$ and $b$ is constant, then its locus will be an ellipse (the red curve in the diagram) with one focus at $a$ and the other one at $b$. The vertical line through $c$ will bisect the angle between the blue lines through $c$ at the point where the tangent to the ellipse is horizontal, as in the diagram. In other words, this happens at the lowest point of the ellipse. As far as I know, there is no purely geometric way of constructing this point.

In physics, if there is a light source at one focus of an ellipse then the light rays from it will all be focused at the other focus. (That is the reason for using the term focus for these points.) This means that the two blue lines from $c$, to $a$ and $b$, make equal angles with the tangent at $c$. Therefore the line perpendicular to the tangent (in this case, the vertical line) bisects the angle between the blue lines.