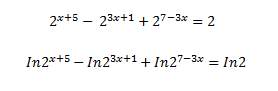Discussion Overview
The discussion revolves around the use of logarithms to solve exponential equations, exploring whether taking the logarithm of both sides is a valid approach. Participants consider the implications of logarithmic properties and alternative methods for solving such equations.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant questions the validity of taking the logarithm of both sides of an exponential equation.
- Another participant asserts that the logarithm of a sum cannot be simplified into the sum of the logarithms of individual terms, which complicates the use of logarithms in this context.
- Some participants agree that while taking the logarithm is a common approach, it may not be useful due to the nature of the equation being discussed.
- A later reply suggests that converting the equation into a polynomial form may be a more effective method for finding solutions, highlighting the importance of exponentiation rules.
- Participants discuss the possibility of finding integer solutions through trial and error and mention the Rational Root Theorem as a potential aid.
- There is mention of polynomial long division and synthetic division as methods to further analyze the polynomial formed from the exponential equation.
- One participant concludes that while logarithms can be used in general cases, the specific problem at hand may require simpler methods for solution.
Areas of Agreement / Disagreement
Participants express differing views on the utility of logarithms for solving the given exponential equation. While some agree that logarithms are not helpful due to the properties of sums, others propose alternative methods without reaching a consensus on the best approach.
Contextual Notes
Participants note limitations regarding the simplification of logarithmic expressions and the specific conditions under which the discussed methods apply. The discussion does not resolve the complexities involved in solving the equation.
Who May Find This Useful
This discussion may be of interest to students and educators in mathematics, particularly those exploring methods for solving exponential equations and the properties of logarithms.