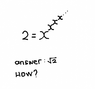Can someone solve this exponential equation for me?
- Context: High School
- Thread starter Ameer Bux
- Start date
Click For Summary
SUMMARY
The exponential equation \(2 = x^{x^{x^{\ldots}}}\) converges to the solution \(x = \sqrt{2}\), as established by Doctor Tom in the forum discussion. The reasoning involves recognizing that the infinite exponentiation can be simplified to \(y = \sqrt{2}^{y}\), leading to the conclusion that \(y\) equals \(2\). However, the discussion highlights the importance of understanding the non-associative nature of exponentiation and the conditions under which such equations converge, particularly emphasizing that \(c\) must satisfy specific inequalities for convergence.
PREREQUISITES- Understanding of infinite exponentiation and limits
- Familiarity with the properties of square roots and exponentiation
- Knowledge of convergence criteria for sequences
- Basic grasp of mathematical constants, particularly \(e\)
- Research the properties of infinite exponentiation and their convergence criteria
- Study the implications of non-associative operations in mathematics
- Explore the mathematical constant \(e\) and its significance in convergence
- Learn about the implications of nested exponentials in calculus and analysis
Mathematicians, students studying calculus or analysis, and anyone interested in the properties of exponential functions and convergence in mathematical sequences.
Similar threads
High School
What went wrong with (-x)^2=x^2?
- · Replies 22 ·
- · Replies 1 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 2 ·
- · Replies 17 ·
- · Replies 13 ·
- · Replies 3 ·
- · Replies 21 ·