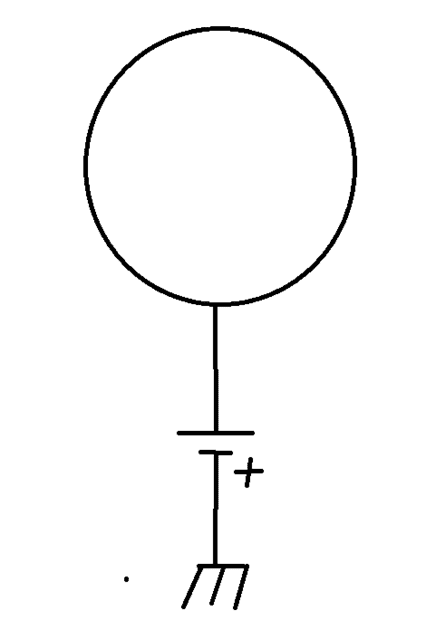Discussion Overview
The discussion revolves around the possibility of fixing the magnetic and electric potentials (A and φ) to zero or some constant value in a region of space. Participants explore the implications of gauge equivalence, the nature of potentials in electromagnetism, and the conditions under which these potentials can be considered constant.
Discussion Character
- Debate/contested
- Technical explanation
- Conceptual clarification
Main Points Raised
- Some participants suggest that the potentials can be fixed to constant values, questioning if a hollow conducting sphere connected to a voltage source would maintain constant potentials inside.
- Others argue that potentials are only physically meaningful up to gauge equivalence, indicating that they cannot be uniquely determined without gauge fixing conditions.
- A participant points out that while potentials can take constant values in one gauge, they may not correspond to constant values in another gauge.
- Another participant explains that the Lorenz gauge condition allows for the addition of certain functions to the potentials, which can affect their constancy.
- Some participants discuss the implications of gauge invariance in Maxwell's theory, noting that the electromagnetic field is observable while the potentials are not uniquely defined.
- There is a mention of the differential form language in electromagnetism, where adding a differential of a scalar function to the potential does not change the field tensor.
- A participant highlights that the Lorenz gauge is a partial gauge fixing, which leaves residual gauge freedom, affecting the constancy of the potentials.
Areas of Agreement / Disagreement
Participants express differing views on the nature of potentials and their constancy. There is no consensus on whether the potentials can be fixed to constant values, and the discussion remains unresolved with multiple competing perspectives.
Contextual Notes
The discussion includes limitations related to gauge fixing conditions, the ambiguity of potentials in different gauges, and the mathematical implications of gauge invariance. These aspects are not fully resolved within the conversation.