requied
- 98
- 3
- Homework Statement
- Show that the function u=φ(xy) +√xy ψ(y/x)provides the following equation.
- Relevant Equations
- u=φ(xy) +√xy ψ(y/x)
I research about coordinate systems and I found the following informations about transformation.

Now, if I replace arctan (x/y) (according to the picture above) to φ, I think I can solve. But if I can do this, then what will be replaced to ψ? I mean, I know just taking partial derative about this question and I guess this symbols can look familiar someone who spend some times about the topic. I left below a clear picture of question. Thanks for now.
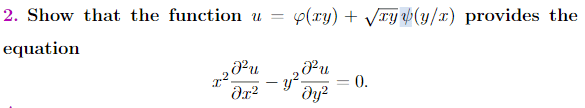
Now, if I replace arctan (x/y) (according to the picture above) to φ, I think I can solve. But if I can do this, then what will be replaced to ψ? I mean, I know just taking partial derative about this question and I guess this symbols can look familiar someone who spend some times about the topic. I left below a clear picture of question. Thanks for now.