Can Zeta ζ(½+it) be interpreted as a Wave function?

In summary, the conversation discusses a new approach to linking the Riemann Hypothesis to Quantum Mechanics using the Zeta function. This approach involves interpreting the wave graph of ζ(½+it) as a wave function and using a complex version of the Parity Operator. However, it is emphasized that the Riemann Hypothesis can only be proved or disproved through mathematics and not through physics. The forum rules also prohibit discussing personal work on this topic.
  • #1
Jason C
1
0
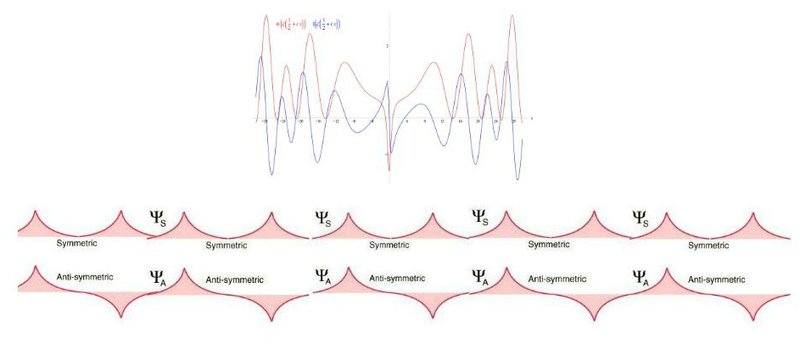
In a recent article by BBM in Physical Review Letters highlights another approach to link QM to Zeta to Prove R.H. There approach proved unsuccessful. I want to ask professional Physicists if the following new approach have merit in connecting the Zeta function to QM? This new line of attack is interpreting the wave graph of ζ(½+it) of Zeta as a wave function. Those wave curves in the graph of ζ(½+it) could be describing the atomic nuclei the Eigenvalue(nontrivial zeros) are related to. It is a new Complex version of the Parity Operator and it is Hermitian. It's eigenvalues can mirror the nontrivial zeros of Zeta. Could this wave function interpretation of ζ(½+it) be the new approach in proving Riemann Hypothesis using Physics? The jpeg attachments are visual representations of this new line of attack for proving RH.
51R5i5BrGQL.jpg

zzzzzxxxx3.jpg
 
Physics news on Phys.org
  • #2
RH is a mathematical statement, so it can be proved (or disproved) only by mathematics. Physics cannot prove RH. Perhaps a proof may be based on some mathematical tool, such as a Hermitian operator, which has applications in physics, but still the proof of RH cannot depend on physics.
 
  • #3
In any case, PhysicsForums is not the place to discuss personal work. Please read the forum rules.

Thread closed.
 

1. What is the Zeta function?

The Zeta function, denoted as ζ(z), is a mathematical function that has applications in number theory and other branches of mathematics. It is defined as the infinite sum of the reciprocal of the nth power of positive integers.

2. What is the significance of ζ(½+it)?

ζ(½+it) is a specific value of the Zeta function at the point ½+it, where t is a real number. This value is of particular interest because it has connections to quantum mechanics and the Riemann hypothesis.

3. How can ζ(½+it) be interpreted as a Wave function?

In quantum mechanics, a wave function is a mathematical function that describes the probability of finding a particle at a specific location. By considering ζ(½+it) as a wave function, it can be interpreted as the probability amplitude of finding a particle in a specific state, where the real part represents the position and the imaginary part represents the momentum.

4. Is there evidence to support the interpretation of ζ(½+it) as a Wave function?

There have been several studies exploring the connections between ζ(½+it) and wave functions, but there is currently no definitive evidence to support this interpretation. Some researchers have found intriguing connections, while others have not. This is still an area of ongoing research and debate.

5. What are the potential implications of ζ(½+it) being interpreted as a Wave function?

If ζ(½+it) can be definitively interpreted as a wave function, it could have significant implications for our understanding of the universe and the nature of reality. It could potentially provide insights into the connection between quantum mechanics and number theory, and shed light on the mysteries of the Riemann hypothesis.

Similar threads

I Connection of zeta to primes: less Euler than error or L-functions?
    • General Math
Replies
2
Views
1K
A Can Bloch Waves Reveal Periodic Potentials in Quantum Mechanics?
    • Quantum Physics
Replies
10
Views
1K
Riemann Zeta Function shows non-trival zeros critical-strip symmetry
    • Calculus and Beyond Homework Help
Replies
1
Views
1K
Riemann Zeta Function Zeros
    • General Math
Replies
1
Views
2K
A Is this a valid physical analogy for the Riemann Hypothesis?
    • General Math
Replies
5
Views
1K
I Role of determinate states in quantum mechanics
    • Quantum Physics
Replies
2
Views
2K
Understanding the Zeta Function and Riemann Hypothesis: A Beginner's Guide
    • Linear and Abstract Algebra
Replies
8
Views
10K
Difficult Zeta Function Proof NEED ANSWER
    • Calculus and Beyond Homework Help
Replies
2
Views
1K
Is Selberg's Zeta Function Proof of the Riemann Hypothesis?
    • Linear and Abstract Algebra
Replies
1
Views
2K
Can someone help me understand and evaluate the Riemann zeta function?
    • Linear and Abstract Algebra
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top