Riemann hypothesis Definition and 74 Threads

Hello PF! If ##\Re (s)## is the real part of ##s## and ##\Im (s)## is the imaginary part, then t is very easy to prove that $$\zeta (s) = \zeta ( \Re (s) ) \zeta ( \Im (s)i) - \displaystyle\sum_{n=1}^\infty \frac{1}{n^{\Re (s)}} [\displaystyle\sum_{k \in S, \mathbb{Z} \S = n}...

[url="https://www.physicsforums.com/insights/the-history-and-importance-of-the-riemann-hypothesis/"]Continue reading...

Continue reading...

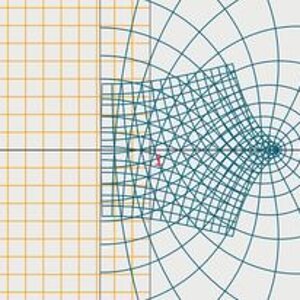
The Riemann Hypothesis, Explained

That there is yet another mathematician (Dr Kumar Eswaran, Hyderabad) claiming to have solved the Riemann Hypothesis is not surprising. That the institute for which he works for (SNIST) is satisfied that the proof is correct is also not surprising. The eyebrows started to lightly ascend upon...

YouTube has been suggesting videos about category theory of late, and I have spent some time skimming through them, without really understanding where it's all going. A question came to mind, namely: It seems reasonably conceivable that group theory could perhaps supply a vital key to the...

This is the Riemann Zeta function ##Z(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}##. It equals 0 only at the negative integers on the real axis and numbers of form ##1/2+x i##. The series can be expanded to this: $$\sum_{n=1}^{\infty} \frac{1}{n^s} = \sum_{n=1}^{\infty} \frac{1}{n^{1/2 + xi}} =...

Often I read that the Riemann Hypothesis (RH) is related to prime numbers because of the equivalence on Re(s)>1 of the zeta function and Eurler's product formula , but is it more accurate that the relevance of the RH to primes (or vice-versa) is either that the RH implies formulas for the...

https://phys.org/news/2019-05-mathematicians-revive-abandoned-approach-riemann.html and more on the Reimann Hypothesis backstory from Numberphile:

Extremely quick question: According to http://mathworld.wolfram.com/PrimeNumberTheorem.html, the Riemann Hypothesis is equivalent to |Li(x)-π(x)|≤ c(√x)*ln(x) for some constant c. Am I correct that then c goes to 0 as x goes to infinity? Does any expression exist (yet) for c? Thanks.

I found the following blog post from a Ph.D., "The Riemann Hypothesis, explained", while trying to get up to speed with the Riemann Hypothesis. It is at, https://medium.com/@JorgenVeisdal/the-riemann-hypothesis-explained-fa01c1f75d3f It seemed well written as I could understand it. Delete or...

I am very baffled. I have heard through the grapevine that the Riemann hypothesis has been proven. My first reaction was of course to dismiss it as yet another failed attempt by someone who was not careful or by a crackpot, or some type of April's fool joke made a few months late.But what I...

The question here is not asking for links to help understand analytic continuation or the Riemann hypothesis, but rather help in understand the bits of hand-waving in the following video’s explanations : https://www.youtube.com/watch?v=sD0NjbwqlYw (apparently narrated by the same person who does...

The number line at x=1/2 is mediated by a concurrent incentive field whose shape can be extrapolated through the placement of prime numbers. Each prime number is a turning point in the n-dimensional movement of the imaginary number line, whose degree and angle can be determined through all the...

In a recent article by BBM in Physical Review Letters highlights another approach to link QM to Zeta to Prove R.H. There approach proved unsuccessful. I want to ask professional Physicists if the following new approach have merit in connecting the Zeta function to QM? This new line of attack...

If the zeta function intersects the critical line when the real part is 1/2, then it will intersect some other line when some other real part is used. Isn't the Riemann Hypothesis just based on a particular convention for the critical line?

Hello! I read some stuff about the Riemann hypothesis and the formulation seems pretty clear. I also read that many proof of it (well basically all of them) are wrong. I was just wondering in which way are they wrong? (I haven't find a page with the wrong proofs, together with explanations of...

Found an article online detailing a proof of the Riemann Hypothesis: << link deleted by mentor - unacceptable source >>

Has anything similar to the Riemann hypothesis ever been solved? Specifically, has anyone proven that the real part of a result of some particular function always assumes a particular value?

http://arxiv.org/abs/1202.2115 I know Arxiv isn't a real journal, but this caught my eye. Is this a meaningful physical interpretation of the Riemann hypothesis? From what I understand, the zeta function can be modeled as a wave, but attempting to solve for the real part requires infinite...

I just thought about the critical concepts in mathematics and physics that arose in the last century: Goedel, Schroedinger, etc. My question is: Are there any physical theories that rely on the validity of the extended Riemann Hypothesis? I don't mean computer science, i.e. secure...

Throughout this note, I'll give a brief, explanatory, informal introduction to the Riemann Hypothesis (RH) explaining the statement of the conjecture, the difficulties of approaching it as well as some notable consequences of RH in the field of number theory. I hope the readers will enjoy the...

The Riemann hypothesis states, whenever the Riemann zeta function hits 0, the real part of the input must be 0.5. Does any input with real part being 0.5 make the function hit 0? Also, assuming the hypothesis is true, would it suffice to prove that if the input's real part is not 0.5, then the...

I saw this in one of the episodes of Numb3rs - (a T.V. show that describes how math can be used to solve crimes) It basically said that if Riemann hypothesis is true then it could break all the internet security. I want to know how. I couldn't understand Riemann hypothesis from Wikipedia and...

what are teh differential equations associated to Riemann Hypothesis in this article ?? http://jp4.journaldephysique.org/index.php?option=com_article&access=standard&Itemid=129&url=/articles/jp4/abs/1998/06/jp4199808PR625/jp4199808PR625.html where could i find the article for free ? , have...

The Riemann hypothesis is arguably the most difficult and perplexing unsolved theorems in all of mathematics. There is currently a $1,000,000 prize for it's solution. It's been 153 years since it's inception in 1859 and no mathematician has ever been able to solve it, not even Bernhard Riemann...

I once had a math professor who said that although they might not admit it, most mathematicians try to solve the Riemann hypothesis in their spare time. How true is this? Who is trying to solve the Riemann hypothesis? I don't just mean "are you?" (although feel free to speak up if you are)...

Happy April fool's day! (Rofl)

I don't know anything of complex analysis or analytic number theory or analytic continuation. But i read about zeta function and riemann hypothesis over wikipedia, clay institute's website and few other sources. I started with original zeta function...

Hey guys, I saw these just showed up on arXiv, published by some unknown who claims to have invented his own number system and is not affiliated with any academic institutions. What do you make of this? http://arxiv.org/abs/1110.3465 http://arxiv.org/abs/1110.2952

let be the function \sum_{\rho} (\rho )^{-1} =Z and let be the sum S= \sum_{\gamma}\frac{1}{1/4+ \gamma ^{2}} here 'gamma' runs over the imaginary part of the Riemann Zeros then is the Riemann Hypothesis equivalent to the assertion that S=2Z ??

I think I have managed to disprove the Riemann Hypothesis. Hope I have not made a calculation error.

Th Riemann Hypothesis states that every 0 lies on x=0.5. What is x here?

How would the world benefit from the Riemann hypothesis being solved? Mathematicians have been trying to solve this for over 100 years, but have been unable to due to it's mind-boggling complexity and difficulty. What would the world benefit if this theorem was to be solved?

Would the field of the number theory collapse or flourish if the Riemann Hypothesis is proved as true?

This could be the way to proof. remember, this is not a proof. today I found a clue to solution to Riemann hypothesis: Let it be Riemann zeta function :ζ(s) The proof that all the non trivial zeroes lie on the critical strip when s = 1/2 + it let us suppose there are other zeroes...

I was wondering if one of the consequences of the Elliott-Halberstam conjecture would imply the Riemann Hypothesis (RH) or the Generalized Riemann Hypothesis (GRH)? Or at least if there is a connection between the Elliott-Halberstam conjecture and RH or GRH? I ask because the...

Maybe someone will find something interesting in this paper. They have a reference to some 1995 work by Alain Connes. I didn't have time to look into this very much. Maybe it's amusing and maybe not: http://arxiv.org/pdf/1012.4665v1

For those not familiar with the term Fermi estimate/problem/question see here: http://www.vendian.org/envelope/dir0/fermi_questions.html http://en.wikipedia.org/wiki/Fermi_problem My question: Between the time that Riemann posed his famous question (in 1859) and now, how many hours have...

hmm...

(Dis)proof of Riemann hypothesis,Goldbach,Polignac,Legendre conjecture I'm just an amateur and not goot at english ^^;

HERE http://vixra.org/pdf/1007.0005v1.pdf is my proposed proof of an operator whose Eigenvalues would be the Imaginary part of the zeros for the Riemann Hypothesis the ideas are the following* for semiclassical WKB evaluation of energies the number of levels N(E) is related to the integral of...

Does anyone know where to find this paper? Formule de trace en géométrie non-commutative et hypothèse de Riemann = Trace formula in noncommutative geometry and the Riemann hypothesis http://cat.inist.fr/?aModele=afficheN&cpsidt=2561461 The purchase link is broken there.. it gets stuck...

http://arxiv1.library.cornell.edu/PS_cache/math/pdf/0102/0102031v10.pdf and http://arxiv1.library.cornell.edu/PS_cache/math/pdf/0102/0102031v1.pdf what do you think ? Author defines 2 operators D_{+} and D_{-} so they satisfy the properties D_{+} = D^{*}_{-} D_{-} = D^{*}_{+}...

Let me start off by saying I have not yet had a formal course in Number Thoery and have only read briefly on the subject...hence the question: How close (in terms that would be understood by someone in my position) is the math community to proving the Riemann Hypothesis? I'm assuming there...

Hi, I'm Yr 13 and just wanted to do some further reading/exploring. So i understand that the zeta function is something to do with summing up like this: 1/ (1^s) + 1/(2^s) etc etc Now, I just want to know what are non-trivial zeros and trivial zeros? I just want to be able to understand this...

Accurate Proof verification of Riemann’s Hypothesis Riemann Hypothesis states that \int \frac{1}{ln (x)} has a root at \frac{1}{2} when s=2 The time series expansion of Log function is, [tex] \ln(x) = \frac {[x-1}{[x-2}+ \frac{1){3} \frac{x-3}{x-4} + \frac{1}{5}\frac{x-5}{x-6}+……...

Well we know what matryoshka dolls are? Those nested dolls one inside another. I am a mere laymen and amateur that's why I am using descriptive terms instead of math rigor. So what should the approach be: If RH nest Hilbert-Polya conjecture, then what things nest HP conjecture? And ad...

Hi All, I would like to present what I believe to be a simple way to convey the essence of the Riemann Hypothesis to High School students. I hope you like it, and reply with suggestions for further improvements. Note for teachers: the rationale behind the graphs lays with the geometric...

...But it may not exist yet. Has any mathematician thought about producing a formula or function which spits out all the prime numbers? i.e 1->2, 2->3, 3->3, 4->5, 5->7, 6->11 etc. Any attempts been made? What the closest that people have thought?