Canoe Velocity Relative to River: 0.413m/s

[zippeh]

Homework Statement

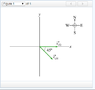
A canoe has a velocity of 0.360m/s southeast (at 315°) relative to the earth. The canoe is on a river that is flowing at 0.580m/s east relative to the earth.

Find the magnitude of the velocity v⃗ c/r of the canoe relative to the river.

Homework Equations

V_x=V₀cos(θ)
V_y=V₀sin(θ)

The Attempt at a Solution

The answer is V_c/r=0.413 m/s and the (V_c/r)x , (V_c/r)y =
-0.325,-0.255 ; respectively.


There are a few things I am confused about with the equations on the problem in general. Firstly, why do these equations work : V_x=V₀cos(θ) and V_y=V₀sin(θ).

I don't understand why I have to use these equations in the problem to obtain the V_x when the problem (to my understanding) gives me V_x and the V_y, which should be the value of V_c/r since this should be just simple vector addition. This is what I am thinking (see attachments). The magnitude of the velocity of V_c/r = V_c/e - V_r/e. So, V_c/e is given at a 315° angle at a velocity of .350m/s. Then using the head to tail method, -V_r/e is given at 180° at a velocity of .580m/s. Using the cos(315°)*.360, I should get -.255 for the magnitude of the velocity of V_c/r instead of .413. I know this is obviously wrong since you can't have a negative velocity in this problem, the way they have the positive and negative planes set up, but I just want to know why the other way works and why it isn't simple vector addition/subtraction. Thanks in advance!

 

[andrevdh]

The velocity of the canoe relative to the Earth is the resultant vector of the canoe's velocity relative to the river and of the velocity of the river relative to the earth.

 

[zippeh]

That doesn't really help me, could you explain more in depth please?

 

[rude man]

v_c/e = v_r/e + v_c/r

Solve the equation for v_c/r by breaking the other two (given) velocities into their x (east) and y (north) components, then take the magnitude of the result. The given answer checks.

NOTE: the given velocity of the canoe w/r/t Earth is not the velocity the canoe would have w/r/t Earth in the absence of river flow. It's the actual canoe-to-earth velocity including the effect of the river flow.

 

[andrevdh]

The canoe's velocity consists of two components. Its velocity relative to the river, that is the person rowing it sees that he is rowing the canoe at a certain speed in a certain direction with respect to the water, but it is also carried by the river at a certain speed in a certain direction. So the canoe's velocity is the resultant of these two velocities.