Can't we use linear regression for classification/prediction?

Click For Summary
SUMMARY

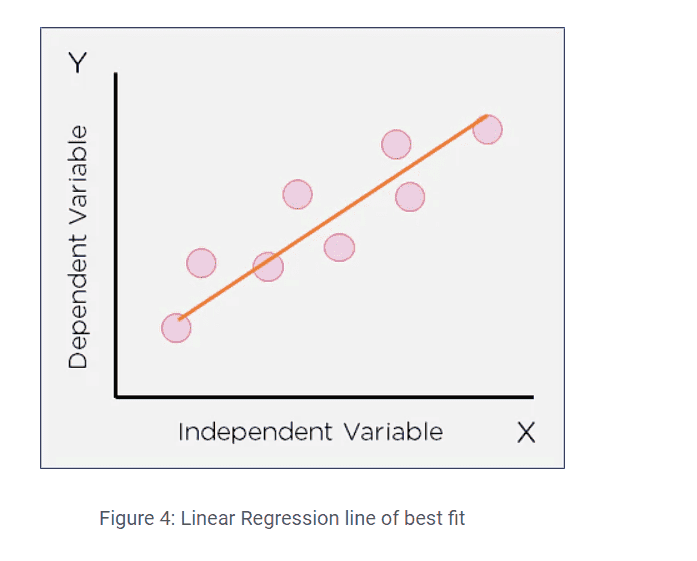
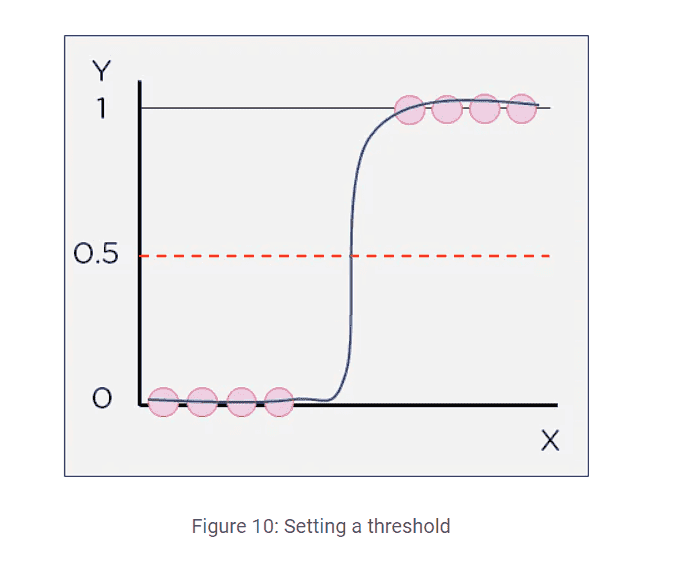
Linear regression is primarily designed for predicting continuous numerical values, while logistic regression is specifically tailored for categorical outcomes. The discussion highlights that while one can apply linear regression to classify binary outcomes (e.g., using a threshold), it is not inherently suited for such tasks due to the nature of linear relationships. The conversation also emphasizes the performance implications of branching in code execution, particularly in low-level programming contexts, and critiques the use of inappropriate examples for threshold curves in classification.

PREREQUISITES
  • Understanding of linear regression and logistic regression concepts
  • Familiarity with binary classification techniques
  • Knowledge of performance implications in programming, especially branching
  • Basic grasp of nonlinear functions and their application in regression models
NEXT STEPS
  • Study the differences between linear regression and logistic regression in depth
  • Explore the implications of branching in programming and its effect on performance
  • Learn about using nonlinear functions in linear regression models
  • Investigate appropriate examples of threshold curves for classification tasks
USEFUL FOR

Data scientists, machine learning practitioners, and software developers interested in understanding the nuances of regression techniques and their applications in classification problems.

shivajikobardan
Messages
637
Reaction score
54
Homework Statement
difference between logistic and linear regression.
Relevant Equations
none
they say that linear regression is used to predict numerical/continuous values whereas logistic regression is used to predict categorical value. but i think we can predict yes/no from linear regression as well

1651852382099.png


Just say that for x>some value, y=0 otherwise, y=1. What am I missing? What is its difference with this below figure?

1651852434225.png
 
Physics news on Phys.org
Branching can have profound effects on performance: for example, the overhead of accessing code modules not currently quickly available after an if/then/else branch. It not as as simple as you might think a priori. Complicated data analysis like you present can have this kind of problem too.

Here is a somewhat dated, but still very important read from Ulrich Drepper:
https://www.akkadia.org/drepper/cpumemory.pdf

I am sure someone will spout reasons why it is "bad", but your question is down in the weeds and low level db programmers are down there in the weeds with you and have to mess with branching effects all the time. I concede that very high level programming platforms can negate some of this. But the question asked above still remains for us weedy types.

Posted in error.
 
Last edited:
jim mcnamara said:
Branching can have profound effects on performance...
Is this the reply to a different thread?
 
shivajikobardan said:
What is its difference with this below figure?
Are you joking? One is a straight line (hence linear regression), the other is an s-curve.

The second plot is a terrible example of a threshold curve BTW - the input data points should not all be 0 or 1 because in that case there is no need to apply the threshold.
 
@pbuk thanks for the correction.
 
pbuk said:
Are you joking? One is a straight line (hence linear regression), the other is an s-curve.
Ofc I get that. What I am trying to say is why can't we say if x>0.5, y=1 else y=0?
pbuk said:
The second plot is a terrible example of a threshold curve BTW - the input data points should not all be 0 or 1 because in that case there is no need to apply the threshold.
 
shivajikobardan said:
Ofc I get that. What I am trying to say is why can't we say if x>0.5, y=1 else y=0?
You can use linear regression with nonlinear functions as long as the form of the model has the parameters of the linear regression in an acceptable way. The values of the nonlinear functions are the independent variables of the linear regression. i.e. ##Y = a_0 + a_1 f_1(X_1) + a_2 f_2(X_2) + \epsilon## is a model where linear regression can be used to find the ##a_i##s even if the ##f_i##s are nonlinear. The values ##z_{i,j}=f_i(x_j)## are the new independent variables.
One limitation on the use of linear regression for classification is that the classifications often can not be defined by a variable, ##X##. How can the categories (man, woman, dog, cat, duck) be defined by a real variable, ##X##?
 
Last edited:
shivajikobardan said:
What I am trying to say is why can't we say if x>0.5, y=1 else y=0?
Because that is not a linear relationship.
 

Similar threads

Undergrad What Are the Key Differences Between OLS and GLM Models in Statistical Analysis?
  • · Replies 3 ·
Replies
3
Views
3K
Linear vs. Cubic Regression: Training and Test RSS Comparison
  • · Replies 10 ·
Replies
10
Views
9K
High School Limitations of Multivariate Linear Regression
  • · Replies 6 ·
Replies
6
Views
3K
Simple overestimate of slope uncertainty in regression
  • · Replies 11 ·
Replies
11
Views
5K
Undergrad Regression line with zero slope and average as best prediction
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Normality of errors and residuals in ordinary linear regression
  • · Replies 3 ·
Replies
3
Views
2K
High School Can We Use Regression Line x on y if y is the Dependent Variable?
  • · Replies 9 ·
Replies
9
Views
2K
Graduate Continuous output: logistic vs linear regression
  • · Replies 4 ·
Replies
4
Views
2K
How Do You Optimize a and b in Linear Regression for Minimal Deviation?
  • · Replies 1 ·
Replies
1
Views
3K
Undergrad Lack of Fit in Ordinal Regression -- Analysis/Alternatives?
  • · Replies 21 ·
Replies
21
Views
3K