Solving the Capacitor Network Problem - Find Ceq = 2C

[Gabriel Maia]

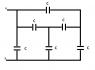
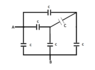
Hi. The problem is: Show that this capacitor network can be reduced to one equivalent capacitor and find its capacitance Ceq. (The network is in the attached image)

I've tried to solve this problem by eliminating the capacitors two by two but it never lead me to the correct answer: Ceq=2C. In fact, I've reached a fair amount of different solutions trying different combinations of capacitor pairs.

My problem is: None of them have a clear association with any other. Neither a parallel nor a series connection. The three inferior capacitors have their inferior plates conected to the potential VB but their superior plates are connected to different potentials. They are not, therefore, connected in parallel.

How do I analyse this system?

Thank you.

 

[UltrafastPED]

You need to use a Y-delta transform: http://en.wikipedia.org/wiki/Y-Δ_transform

Or maybe several of them ...

 

[Gabriel Maia]

I think it will do just fine. Thank you very much.

 

[Gabriel Maia]

Hi UltrafastPED. Thank you for your time. I'm not familiar with the Y-delta transform so I tried it on a network that seemed to me a little easier. The thing is I'm still having trouble. I have sketched my procedure. It is in the attached image.



The original network is the one with the capacitors C1, C2, C3, C4 and C5. C1, C2 and C3 form a delta, which can be transformed into a Y where

C1'=(C2C3+C3C1+C1C2)/C1

C2'=(C2C3+C3C1+C1C2)/C2

C3'=(C2C3+C3C1+C1C2)/C3

right?

I believe my problem is "how does the Y connects to the rest of the network?". It seemed to me that C1' and C5 should be connected in series. Same for C2' and C4. The two equivalent capacitors obtained from these two series would then be connected in parallel with each other. Finally, the result of this parallel connection should be connected in series with C3'.

In my problem C1=C5=C and C2=C3=C4=2C. The answer should be 10C/7 and I'm not understanding why I'm not getting there.

 

[Saitama]

No need to apply Y-Delta transforms or other dirty transformations. :tongue2:

See attachment. There is a wheat stone bridge hanging around.

 

[Gabriel Maia]

Sorry... I'm not following you. Inside the big square there are three capacitors. The capacitor at the bottom and the one to the right are on the bridge. Right?

This allows me to know the difference of potential between B and the upper right corner of the big square, right?

I'm failing to see how the connection go then to form an equivalent capacitor for the network.

 

[Saitama]

Sorry... I'm not following you. Inside the big square there are three capacitors. The capacitor at the bottom and the one to the right are on the bridge. Right?

Can you please indicate it on the diagram? I can't follow this.

 

[eprofu]

< Mentor Note -- providing solutions to homework questions is normally not allowed, but in this case the thread is years old, so the student has moved on. Showing this solution for future student reference is okay in this case. >