Romain Nzebele
- 21
- 0
- Homework Statement
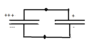
- A 25.0-mF capacitor and a 40.0-mF capacitor are charged by being connected across separate 50.0-V batteries. (a) Determine the resulting charge on each capacitor. (b) The capacitors are then disconnected from their batteries and connected to each other, with each negative plate connected to the other positive plate. What is the final charge of each capacitor?
- Relevant Equations
- C=Q/V
I have no problems with part a). I used the formula for capacitance and determined the charges to be 0.00125 coulombs and 0.002 coulombs. The solution in the book is the same. For part b) my initial thought was that the charges will redistribute themselves so that each capacitor get the same charge. So I wrote that each capacitor will have (0.00125+0.002)/2=0.001625 coulombs. The solution in the book is very different.