Ranking charge stored on three capacitors by a battery

[ChiralSuperfields]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

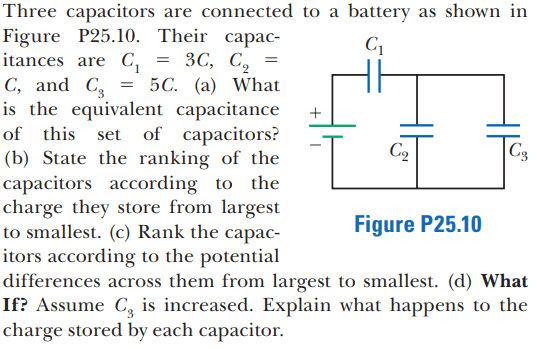
The solution is,

I have a few questions about parts of the solutions,

- Part(b):

(1) Why do they assume that the capacitors are initially uncharged? Do they even need to make that assumption because it seems clear to me that we are finding the charge stored by each capacitor once the circuit has reached steady state. Would it not be better to say assume capacitors $C_1$, $C_2$ and $C_3$ are charged?

(2) How did they get $Q_1 > Q_3 > Q_2$? I don't understand their statement about if the capacitors are initially uncharged then $C_1$ stores the same charge as $C_2$ and $C_3$ in steady state. I though the answer should be $Q_2 < Q_1 < Q_3$ as it should be in the order from smallest to largest capacitance since $Q ∝ C$ (from $C = \frac {Q}{V}$), correct?

- Part(d):

(3) I don't understand why the charge $Q$ increases from $Q_i$ to $Q_f$. I thought charge would be conserved in this circuit, why is it not conserved?

Many thanks!

 

[kuruman]

They don't have to assume that the capacitors are initially uncharged. I can see why the ranking done conceptually could be confusing to you. Perhaps you can do it by actually solving for the charges and the voltages. Remember that the sum of voltage drops and rises around a closed loop is zero.

as it should be in the order from smallest to largest capacitance since $Q \propto C$

If you compare charge stored in capacitors, the capacitor with the larger capacitance is guaranteed to hold more charge only if the voltage across the capacitors is the same. In $Q=CV$, if you want to compare $Q$s you cannot only look at $C$ and ignore $V$.

 

[ChiralSuperfields]

They don't have to assume that the capacitors are initially uncharged. I can see why the ranking done conceptually could be confusing to you. Perhaps you can do it by actually solving for the charges and the voltages. Remember that the sum of voltage drops and rises around a closed loop is zero.If you compare charge stored in capacitors, the capacitor with the larger capacitance is guaranteed to hold more charge only if the voltage across the capacitors is the same. In $Q=CV$, if you want to compare $Q$s you cannot only look at $C$ and ignore $V$.

Thank you for your reply @kuruman ! Thank you for reminding me for looking at $V$!

So in terms of proving their ranking $Q_1 > Q_3 > Q_2$ symbolically, do you know what steps I have done wrong please?

Finding the equivalent capacitance of the circuit,

$C_{eq} = 2C = \frac {Q}{V_1 + V_2 + V_3} = \frac {Q}{\epsilon}$

Adding up the positive charge on each plate,

$Q_1 + Q_2 + Q_3 = Q$

Applying KVL to circuit,

$\epsilon = V_1 + V_2 + V_3$

$\epsilon = \frac {Q_1}{C_1} + \frac {Q_2}{C_2}+ \frac {Q_3}{C_3}$

$\frac {Q}{2C}= \frac {Q_1}{C_1} + \frac {Q_2}{C_2}+ \frac {Q_3}{C_3}$

$\frac {Q_1 + Q_2 + Q_3}{2C} = \frac {Q_1}{C_1} + \frac {Q_2}{C_2}+ \frac {Q_3}{C_3}$

$\frac {Q_1 + Q_2 + Q_3}{2C} = \frac {Q_1}{3C} + \frac {Q_2}{C}+ \frac {Q_3}{5C}$

$\frac {Q_1 + Q_2 + Q_3}{2C} = \frac {5Q_1C^2 + 15Q_2C^2 + 3Q_3C^2}{15C^3}$

$7.5C^2(Q_1 + Q_2 + Q_3) = 5Q_1C^2 + 15Q_2C^2 + 3Q_3C^2$

$7.5Q_1 + 7.5Q_2 + 7.5Q_3 = 5Q_1 + 15Q_2 + 3Q_3$

Many thanks!

 

[kuruman]

I don't think you know what you are doing. The first thing you need to do is to identify which capacitors are in series and which are in parallel, not assume that they are all in series which is what your equations say. This identification is done for you in the solution which you ignored for some reason. Your application of KVL is incorrect. You just don't set the sum of all possible potential differences equal to the battery voltage. If you don't remember how to use KVL, please read up on it.

 

[ChiralSuperfields]

I don't think you know what you are doing. The first thing you need to do is to identify which capacitors are in series and which are in parallel, not assume that they are all in series which is what your equations say. This identification is done for you in the solution which you ignored for some reason. Your application of KVL is incorrect. You just don't set the sum of all possible potential differences equal to the battery voltage. If you don't remember how to use KVL, please read up on it.

Thank you for your reply @kuruman!

$C_1$ is in series with the battery
$C_2$ and $C_3$ is in parallel with the battery

Since $C_2$ and $C_3$ are parallel to each other their equivalent capacitance is $C_2 + C_3$.

I think what I did wrong with KVL was that I did not finding the equivalent capacitance of the capacitors in parallel.

So if I replace branch's $C_2$ and $C_3$ with $C_{23}$ I get:

So now $V_1$ and $V_{23}$ oppose the source, I think.

$\epsilon - V_1 - V_{23} = 0$
$\epsilon = V_1 + V_{23}$

So I think what I did wrong was that I applied KVL for the whole loop.

Many thanks!

 

[kuruman]

That's much better.

 

[ChiralSuperfields]

That's much better.

Thank you @kuruman !