Center Frequency and Bandwith of Bandpass Filter?

[Gwozdzilla]

Homework Statement

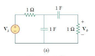
Determine the center frequency and bandwidth of the bandpass filter.

Homework Equations

center frequency of bandpass filter = ω_c occurs when the magnitude of H = 1

H = V₀/V_s

Center frequency occurs when Im(Z) = 0
Z_c = 1/(jωC) = 1/s
Z_L = jωL
Z_R = R

I don't know a formula for finding bandwidth.

The Attempt at a Solution

Z_series = 1 + 1/s
Z_ll = ((1/s)(1 + 1/s))/(2/s + 1)
Z_eq = 1 + Z_ll
Simplifying gives...
Z_eq = (1 + 3s + s²)/(2s + s²)

V_s = IZ_eq
V_ll = IZ_ll
V₀ = I₂(1Ω)
V_series = I₂Z_series = V_ll

V₀Z_series = V_ll = IZ_ll

V₀Z_series = (V_sZ_ll)/Z_eq

V₀/V_series = Z_ll/(Z_eqZ_series)

Plugging in values from above and simplifying gives...

V₀/V_series = s/(s + 3s + 1) = H

s² = -ω²

How do I find the magnitude of H? What is a bandwidth?

 

[rude man]

First thing you should do is label the components R1, C1, C2, R2 left to right. Then work with these symbols.

Then: your H(s) can't be right since it has gain = 1/4 at high frequencies whereas the network H(s) must have zero gain there, thanks to C1.

 

[BvU]

Hello GZ,

Took me a while too to untangle this. In the mean time Rudy chipped in, but here's my 2 cents as well:

It would have been easier for me (and probably for others too) if you would have told us what you mean with the various symbols.

Up to V_series= ... I agree. Then V₀ Z_series=V_ll x (1Ω) otherwise the dimensions don't fit. But numerically you're still good.

V₀/V_series = Z_ll x (1Ω)/(Z_eqZ_series) is something you could have gotten more straightforward as

V₀/V_|| = 1Ω / Z_series multiplied with

V_||/V_s = Z_ll / Z_eq​

The typo that distracted Rudy demonstrates your derivation is a bit complex (too many Z, too many inversions and then inverting again). Never mind.

Magnitude of H follows from $\sqrt{ H^{\displaystyle ^*} H }$ as with all complex numbers.

(At first, LaTeX let me down here, with $H^{\displaystyle ^*}$ I mean the complex conjugate of $H$ )Bandwith is $| \omega_1 - \omega_2 |$ where $H^2(\omega_{1,2}) = H^2_{max}/2$

 

[Gwozdzilla]

So from my value for H = s/(s² + 3s + 1), I can convert back to using jω:

H = (jω)/(-ω² + 3jω + 1)
H = (jω)/(3jω + (1-ω²))

The complex conjugate of the denominator is then 3jω - (1-ω²). I can multiply the numerator and denominator by this and simplify to get:
H = ((ω²-1)(jω) - 3ω²)/(-9ω² -1)

√(H*H) = 1 → H*H = 1

((ω²-1)(jω) - 3ω²)/(-9ω² -1) = 1
(ω²-1)(jω) - 3ω² = -9ω² -1
Simplifying gives the quadratic equation:
(6 + j)ω² - jω + 1 = 0
The quadratic equation gives the result:
ω = -.0219 -.331j

I don't think I did that right. Did I determine the complex conjugate incorrectly?

So for the bandwidth, am I supposed to find dH/dω = 0, and plug that ω back into find H_max, then solve H_max²/2 or am I misunderstanding?

 

[rude man]

So from my value for H = s/(s² + 3s + 1), I can convert back to using jω:
H = (jω)/(-ω² + 3jω + 1)
H = (jω)/(3jω + (1-ω²))
The complex conjugate of the denominator is then 3jω - (1-ω²). I can multiply the numerator and denominator by this and simplify to get:
H = ((ω²-1)(jω) - 3ω²)/(-9ω² -1)
√(H*H) = 1 → H*H = 1
((ω²-1)(jω) - 3ω²)/(-9ω² -1) = 1
(ω²-1)(jω) - 3ω² = -9ω² -1
Simplifying gives the quadratic equation:
(6 + j)ω² - jω + 1 = 0
The quadratic equation gives the result:
ω = -.0219 -.331j
I don't think I did that right. Did I determine the complex conjugate incorrectly?

You never performed HH*. When you multiply numerator & denominator of H(jw) by the cc of the denominator you wind up with the original H(jw), not the cc

.
So for the bandwidth, am I supposed to find dH/dω = 0, and plug that ω back into find H_max, then solve H_max²/2 or am I misunderstanding?

You compute |H| = √|H(jw) H*(jw)|, which is the magnitude of H(jw) and is a real number.
You can then set d|H|/dw = 0 to solve for w of |H|. Plug into |H| and you get |H_max|. Then set |H| = 1/√2 H_max and solve for w again. This time you get two w. Rest is as BvU stated.

 

[Gwozdzilla]

How do I find the complex conjugate of something in the form of (jω)/(3jω + (1-ω²))? I don't see how to simplify it into an x + iy form.

Is the complex conjugate (-jω)/(3jω - (1-ω²))?
If this is the complex conjugate then I get...

√[(jω)/(3jω + (1-ω²))][(-jω)/(3jω - (1-ω²))] = 1

[(jω)/(3jω + (1-ω²))][(-jω)/(3jω - (1-ω²))] = 1
Simplifying gives...
ω⁴ + 8ω² + 1 = 0 which only has imaginary roots, so it's probably also wrong.

 

[BvU]

No need to simplify. Just replace every instance of j by $-$j

 

[BvU]

So for the bandwidth, am I supposed to find dH/dω = 0, and plug that ω back into find Hmax, then solve Hmax2/2 or am I misunderstanding?

That's the idea. ($d|H|\over d\omega$ you mean, of course ... ).

 

[Gwozdzilla]

Okay, so when I replace every instance of j by -j, the complex conjugate is (-jω)/(-3jω + (1-ω²)).

[(jω)/(3jω + (1-ω²))][(-jω)/(-3jω + (1-ω²))] = 1²

This simplifies to 0 = ω⁴ + 6ω² + 1
so ω = ±j(.414) and ω = ±j(2.414)

Is this part correct?

 

[rude man]

Okay, so when I replace every instance of j by -j, the complex conjugate is (-jω)/(-3jω + (1-ω²)).

[(jω)/(3jω + (1-ω²))][(-jω)/(-3jω + (1-ω²))] = 1²

Why are you setting |H|² = 1?

 

[Gwozdzilla]

Why are you setting |H|² = 1?

I thought that a bandpass filter was defined as having its |H(ω_c)| = 1. Is this not the case?

 

[BvU]

Check it out ! You already have an expression for $|H(\omega)|$

 

[rude man]

I thought that a bandpass filter was defined as having its |H(ω_c)| = 1. Is this not the case?

No it isn't. You need to go d|H|/dw = 0, solve for w, replace in |H|.

 

[Gwozdzilla]

|H(ω)| = [(jω)/(3jw + (1-ω²))][(-jω)/(-3jw + (1-ω²))]
|H| = ω²/(7ω² + ω⁴ + 1)

d|H|/dω = 2ω(7ω² + ω⁴ + 1)^-1 -ω²(7ω² + ω⁴ + 1)^-2(14ω + 4ω³) = 0
Simplifying gives ω = 1. Is this the center frequency?

|H(1)| = 1/9 Is this the bandwidth?

 

[rude man]

|H(ω)| = [(jω)/(3jw + (1-ω²))][(-jω)/(-3jw + (1-ω²))]
|H| = ω²/(7ω² + ω⁴ + 1)

d|H|/dω = 2ω(7ω² + ω⁴ + 1)^-1 -ω²(7ω² + ω⁴ + 1)^-2(14ω + 4ω³) = 0
Simplifying gives ω = 1. Is this the center frequency?

Yes, if you did the math correctly. I did not check it.

|H(1)| = 1/9 Is this the bandwidth?

No. |H|(1) = max. gain.
I did not check your math but your approach is correct up to then.
Follow what I said in post 5 near the end to get the bandwidth.

 

[Gwozdzilla]

|H(ω)| = ω²/(7ω² + ω⁴ + 1) = (1/√2)H_max = 1/(9√2)

Solving for ω gives ω = ±2.355 and ±.425

Bandwidth = B = ω₂ - ω₁ = 2.78 or 1.93

Is this correct?

 

[rude man]

|H(ω)| = ω²/(7ω² + ω⁴ + 1) = (1/√2)H_max = 1/(9√2)

Solving for ω gives ω = ±2.355 and ±.425
Bandwidth = B = ω₂ - ω₁ = 2.78 or 1.93

Is this correct?

ω cannot be negative, at least not for you now.
Otherwise, looks right if you did the math right.
Check #1: does |H| → 0 as ω → 0? Yes.
Check #2. does |H| → 0 as ω → ∞? Yes.
Check #3: does √(ω₁ω₂) = ω₀ = 1? √[(2.355)(0.425)] = 1. Yes. (This test rests on what I state below in my last sentence. So you most probably got the mid-band and corner frequencies right.

EDIT: But it's not sure. What you can say is that if √(ω₁ω₂) is not = ω_max then you got something wrong. In other words, it's a necessity but not a sufficiency test.)

So, H is a bandpass, since gain is zero at DC (ω=0) and at arbitrarily high frequencies, and gain > 0 somewhere inbetween.
But you don't have the right answer for bandwidth. Bandwidth is the width of the passband around the peak, with rolloff frequencies at gain = |H_max|/√2 on either side of the max. frequency ω₀. If you're using log paper (for the x axis), the two points w1 and w2 are equidistant from w₀. ω₀ is the geometric mean between ω₁ and ω₂. So take another shot at bandwidth.

 

[Gwozdzilla]

Bandwith is $| \omega_1 - \omega_2 |$ where $H^2(\omega_{1,2}) = H^2_{max}/2$

If I know that ω₁ and ω₂ are correct by calculating that √ω₁ω₂ = 1, and I know that I should take the positive values of ω_1,2, then why isn't the bandwidth = |ω₁-ω₂| = |.425-2.355| = |-1.93| = 1.93?

 

[rude man]

If I know that ω₁ and ω₂ are correct by calculating that √ω₁ω₂ = 1, and I know that I should take the positive values of ω_1,2, then why isn't the bandwidth = |ω₁-ω₂| = |.425-2.355| = |-1.93| = 1.93?

I said ω is always > 0 but you still got the same right answer: bandwidth = 2.355 - 0.425 = 1.93 rad/s.

BTW look again at my post #17. I edited it a bit.