Centrifuge for astronaut training (tangential and normal acceleration)

[badaboom]

Homework Statement

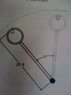
A centrifuge used for astronaut training starts moving from rest with a velocity Vi=8.5t[ft/sec]. It is know that a person loses consciousness when experiences an acceleration in the order of 10g. determine:

a)how long can hold the astronaut in the centrifuge before losing consciousness

b)the velocity of the astronaut

c)the normal and tangential acceleration of the astronaut

Homework Equations

normal acceleration = V²/20
tangential acceleration = v^.
V₁² =Vo² + 2(tang. acceleration) * (s1-s0)

The Attempt at a Solution

I got the normal acceleration, (3.6125), but I don't know how to get the tangential acceleration since I don't have an initial OR final position. Any help?

 

[badaboom]

anyone?

 

[gneill]

You haven't completely specified the problem. What's the radial length of the centrifuge arm?

 

[badaboom]

that's in the picture, it's 20ft long

 

[gneill]

What do you mean when you say that you 'got the acceleration'? Which acceleration would that be? (there are no units on your number, and no evidence of how you arrived at it).

The centripetal acceleration (or centrifugal if you prefer) is going to change with time, along with the angular velocity of the centrifuge and the velocity of its outer edge. That's why the problem gives the velocity as a function of time.

 

[badaboom]

then forget about it, I think ti was wrong. Can u help?

 

[gneill]

It seems to me that the questions posed should be answered in reverse order ((c), (b), (a)).

Why don't you start by drawing a free body diagram of all the accelerations affecting the astronaut? Then write expressions for each as functions of time.

 

[badaboom]

ok, I got tangencial acceleration with at=dv/dt, it was 8.5, normal acceleration I got with V^2/R, which was 3.6125t^2. I have the free body diagram with only those two forces acting on the astronaut. What now?

 

[gneill]

Are there any other accelerations working on the astronaut? Is the centrifuge floating free in space, or is it here on Earth?

 

[badaboom]

It's here on Earth obviously, does that mean I have to include gravity too? Are the other two accelerations right? How does gravity affect the astronaut? :S

 

[gneill]

It's here on Earth obviously, does that mean I have to include gravity too? Are the other two accelerations right? How does gravity affect the astronaut? :S

The other accelerations appear to be fine.

Accelerations are vectors. How would you go about determining the magnitude of their resultant?

 

[badaboom]

well the magnitude would be the sum of them, each of them squared, and the squared root of that. sqrt(72.25 + 13.05t^4). Do I integrate this and get the velocity now?

 

[gneill]

Okay, assuming that you're not including gravitational acceleration, you now have a function of t that expresses the magnitude of the acceleration that the astronaut will experience (how would you include gravity in this?).

For part (a) you want to find the time t when he will reach the maximum allowable acceleration.

As for the velocity, you found the function that describes his tangential speed before. This direction of this speed will vary as the centrifuge goes around. Perhaps a better way to express the astronaut's velocity would be as his angular velocity.

 

[badaboom]

angular velocity is V/r, is that V the one given to me, Vo?

 

[gneill]

angular velocity is V/r, is that V the one given to me, Vo?

It changes with time, just as V does (the centrifuge is speeding up). Write it as a function of time.

 

[badaboom]

ok, then the angular velocity is the function 0.425t. But I still don't know how to relate that with the acceleration...

 

[gneill]

You've already derived an expression for the magnitude of the acceleration with respect to time: sqrt(72.25 + 13.05t^4) (ignoring gravity). When will this acceleration reach the maximum allowed?

 

[badaboom]

Ok, I think I got it, sqrt(72.25 + 13.05t^4) has to equal 10g(98.1). I tried to find the value of t and got 5.201s, isn't that too small for this exercise?

 

[gneill]

Make sure that you specify g in the same units that you've been using for the equations.

 

[badaboom]

I've only used g to get 98.1, and the time is always in seconds. Do you think the answer I got is wrong?

 

[gneill]

98.1 what? What are the units?

 

[badaboom]

ft/s^2, but is what I did right?

 

[gneill]

10g is not 98.1 ft/s^2.

10g is 98.1 m/sec^2 --> 322 ft/sec^2 (approx.)

Beware of units!

 

[badaboom]

ok, then the time is 9.4395 and the velocity 4.0118?

 

[gneill]

The time is in the right ballpark (I carried more significant figures through the calculations and came up with 9.41 seconds). 4.0 rad/sec looks like a good angular velocity. It corresponds to a tangential velocity of about 80 ft/sec.

Always be sure to specify the units on your results! Your instructor may choose to take some points off if you don't.

 

[badaboom]

ok, so what I have is the astronaut can continue for 9.4395 seconds, the angular velocity of the astronaut is 4.0118 rad/s^2, the normal acceleration would be 3.6125t^2 and tangencial acceleration is 8.5 rad/s^2. Does that seem about right?
Thank you!

 

[gneill]

ok, so what I have is the astronaut can continue for 9.4395 seconds, the angular velocity of the astronaut is 4.0118 rad/s^2, the normal acceleration would be 3.6125t^2 and tangencial acceleration is 8.5 rad/s^2. Does that seem about right?
Thank you!

You'll probably want to plug your value for t into the expression for the normal acceleration and provide that too; The question wasn't specific about what whether it wanted a particular value or an expression as a function of time. Cover your bases!

Tangential acceleration should be specified in ft/sec^2, since it's a linear measure. You could also provide the tangential velocity along with the angular velocity, just to be safe.

You might want to go easy on the significant digits in the results; they should be in line with the number of significant figures in the given data. I don't know how picky your instructor will be about these things.