Centripetal Acceleration along a curve

[rexorsist]

I've spent hours on this question:

A truck of mass 4500 kg is traveling in a fog due north at 20 m/s. Suddenly, at point A, the driver notices a wall straight ahead. He makes a sharp right turn along path AB, which is one-quarter of a circle of 50 m radius. He does this without any change in speed. From B to C he slows down uniformly, arriving at C with a velocity of 14 m/s [E]. The trip from A to C takes 5.8 seconds.

I made a diagram:

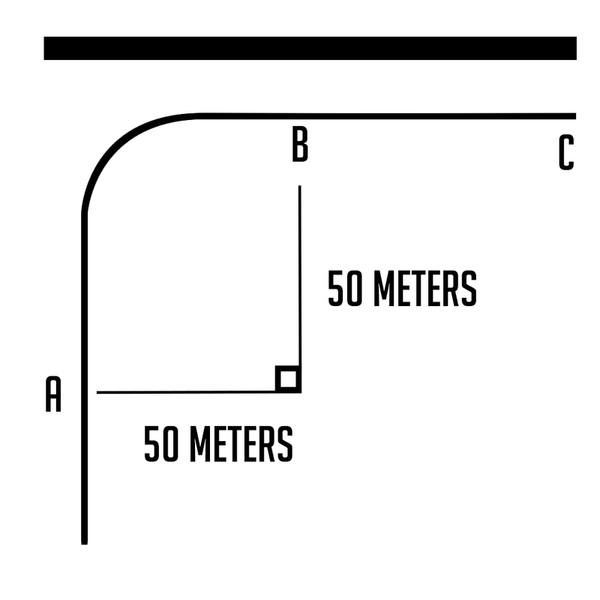
Calculate:

(a) the average acceleration of the truck from A to C,

(b) the average velocity of the truck as it travels from A to C.

I figured to find average velocity first, so I drew a line from point A to point C, and using the the equation of d=((V1-V2)/2)xT, I found the distance between B and C, and calculated the displacement from A to C. Then I divided it by change in Time (5.8s) to find velocity, giving me 16.53 m/s.

To find acceleration, I think I need to use the equation a=v^2/R. However, there is no radius since I extended the displacement.

Is what I'm doing correct? I desperately need help and can't determine if what I'm doing is right or wrong.

 

[Simon Bridge]

You are thinking only in terms of magnitudes - acceleration, velocity, and displacement, are all vectors.
How do you add and subtract vectors?

Note: you are told the radius of the turn. You just didn't draw it properly.

 

[rexorsist]

You are thinking only in terms of magnitudes - acceleration, velocity, and displacement, are all vectors.
How do you add and subtract vectors?

Note: you are told the radius of the turn. You just didn't draw it properly.

Yes, but in order to find the displacement between A and C, I drew a line connecting the two, forming a right angle triangle. The vertical distance to C was 50m. However, I used the motion equation to find the horizontal distance of the triangle. Then I calculated the hypotenuse to get a displacement value of 95.86 m. This was this divided by time to get velocity.

But since I extended the radius, I can't use it any more.

Am I making sense?

If not, can you give me some direction to figure out the acceleration?

 

[rtsswmdktbmhw]

You have found the magnitude of average velocity, but your answer is incomplete because velocity is a vector.

a = v^2/R applies for circular motion. Is the overall motion in your question circular?

 

[rexorsist]

You have found the magnitude of average velocity, but your answer is incomplete because velocity is a vector.

a = v^2/R applies for circular motion. Is the overall motion in your question circular?

No, its not circular when including C,..so does that mean that a=V^2/R doesn't apply in this case? So that means I would simply use a motion equation to determine acceleration?

Also, why is mass mentioned in the question? does it have a significance?

 

[Simon Bridge]

But since I extended the radius, I can't use it any more.

You don't need to extend the radius.

If not, can you give me some direction to figure out the acceleration?

eg. the average acceleration between A and C is the change in velocity over the change in time.
The velocities and times are given to you - no need to work out a displacement.

 

[Simon Bridge]

No, its not circular when including C,..so does that mean that a=V^2/R doesn't apply in this case?

v^2/r only applies for circular motion ... this is not circular motion, therefore ...

So that means I would simply use a motion equation to determine acceleration?

You could, that may work, or you could just apply the definition of average acceleration.
You will have something about that in your notes - probably quite early on in mechanics.

Usually $\vec a_{ave}=\Delta\vec v/\Delta t,\;\vec v_{ave}=\Delta\vec s/\Delta t$.

Also, why is mass mentioned in the question? does it have a significance?

The problem is testing your understanding of what "average acceleration" and "average velocity" means.

There are a number of ways you could misunderstand the problem, some of which would need the mass. i.e. you could attempt to find an equation of motion using Newton's Laws. You could still end up with the correct answer though - so your teacher is being kind, sort of, by allowing you to explore the problem completely.

IRL: you often have more information than you need to solve a problem - so you need to learn to sort out the relevant from the irrelevant information.