Centripetal acceleration and tangential velocity of an object that revolves and rotates

[user079622]

Homework Statement

I must find centripetal acceleration and tangential velocity, I post this to check my results.

Relevant Equations

vt = ω r
ac = ω2 r

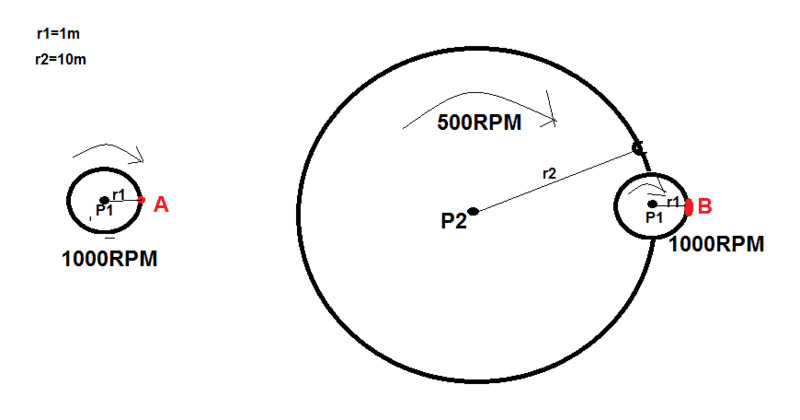
Right picture is two turn tables on of top of the other, smaller turn table is connected with shaft to bigger one so it rotate around itself and in same time "revolve" around center of bigger one which is also rotate about itself. They both rotate clockwise.

I observe case from inertial frame of reference, earth. I must find centripetal acceleration and tangential velocity in point B.

r1=1m ω1=1000RPM
r2=10 ω2=500RPM

Tangential velocity in point B = tangen. velocity in point P1(right picture) + tangen. velocity in point A
vt = ω r
A= 104.72 m/s
P1=523.6 m/s

They are two parallel velocity vectors pointing in same direction so I add them to get tangential velocity in point B=628.32 m/s

Centripetal acceleration in point B = cent. accleration in point P1(right picture) + cent. acceleration in point A

ac = ω2 r
P1= 27416 m/s2
A= 10966 m/s2

They are two vectors that point in same direction,(toward left at my graph), I add them to get centripetal acceleration in point B= 38382 m/s2

Is my logic and results correct?
Point A show case where smaller turn table rotate just around itself, revolution is zero)

 

[haruspex]

Looks fine to me.

 

[user079622]

Looks fine to me.

Do you maybe have any doubts about the way how I calculated centripetal acceleration?

 

[haruspex]

Do you maybe have any doubts about the way how I calculated centripetal acceleration?

Let me think on it some more…
A sanity check: consider $\omega_1=\omega_2$.
Now B is always at $r_1+r_2$ from $P_2$, so its acceleration is clearly $(r_1+r_2)\omega^2$. Your method gives $r_1\omega^2+r_2\omega^2$, which is the same.
Try $\omega_1=0$.

 

[user079622]

Let me think on it some more…
A sanity check: consider $\omega_1=\omega_2$.

In this case is easy and clear.

 

[haruspex]

So are you reassured?

 

[user079622]

So are you reassured?

If ω1=ω2 then vt=576 m/s and acc=30159 m/s2
This is moon case, like small table is locked so it cant rotate in relation to big one.

 

[haruspex]

If ω1=ω2 then vt=576 m/s and acc=30159 m/s2
This is moon case, like small table is locked so it cant rotate in relation to big one.

Yes, but the point of considering such special cases is to see whether your approach in post #1 works. Don't plug in any numbers. I showed in post #4 that your method gives the right formula for that case. Can you do the same for $\omega_1=0$?

 

[user079622]

Yes, but the point of considering such special cases is to see whether your approach in post #1 works. Don't plug in any numbers. I showed in post #4 that your method gives the right formula for that case. Can you do the same for $\omega_1=0$?

Formula for my case is r1 (ω1)2 + r2 ( ω2)2

I must think...
If ω1=0, that mean small table not rotate from earth frame,so point B always point toward right side
If is not rotate then acc=0 from rotation, so it has only acceleration from "revolution" around point P2, that is equal
(r1+r2 ) (ω2)2

But small table then rotate in relation to big table at -500RPM.
Am I correct?

 

[haruspex]

If is not rotate then acc=0 from rotation, so it has only acceleration from "revolution" around point P2, that is equal
(r1+r2 ) (ω2)2

That would conflict with your general solution. Plugging $\omega_1=0$ into $r_1\omega_1^2+r_2\omega_2^2$ gives $r_2\omega_2^2$, not $(r_1+r_2)\omega_2^2$.
But fortunately your reasoning in post #9 is wrong. If $\omega_1=0$, what point is B orbiting?

 

[user079622]

That would conflict with your general solution. Plugging $\omega_1=0$ into $r_1\omega_1^2+r_2\omega_2^2$ gives $r_2\omega_2^2$, not $(r_1+r_2)\omega_2^2$.
But fortunately your reasoning in post #9 is wrong. If $\omega_1=0$, what point is B orbiting?

Yes I miss orbit path
B orbit around point P2+r1
so acc= r2 (ω2)2

 

[haruspex]

Yes I miss orbit path
B orbit around point P2+r1
so acc= r2 (ω2)2

Right. So your solution in post #1 looks to be good.

 

[user079622]

Right. So your solution in post #1 looks to be good.

Thanks for help.