Centripetal Motion Help

[lord_blurg]

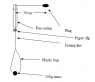
I am currently doing a practical concerning centripetal motion and I am a bit confused. The attachment has the setup of the experiment.

Now the aim of the experiment is to create a horizontal centripetal motion with plug.

If we were to add more mass to the plastic bag would it increase the acceleration of the centripetal motion thus giving us a slightly lower time for a complete revolution of the plug.

I appreciate any help with this matter.

 

[Doc Al]

The more mass in the bag, the faster you'll have to spin the plug. The weight of the bag creates the tension in the line, which provides the centripetal force on the plug.

Did you have a specific question?

 

[magnetar]

From the point of my view:The more mass in the bag, the shorter of the radius! According to the "conservation of angular momentum" the angular velocity is more faster! So giving us a slightly lower time for a complete revolution of the plug.

(I am a foreigner! my english is very poor!)

 

[Doc Al]

Perhaps you should describe exactly what the experiment is doing. It's certainly true that once you get the plug twirling, if you then shorten the radius the angular speed will increase.

Can you express the conservation of angular momentum mathematically?

 

[lord_blurg]

The point of the experiment is to find the relationship between 1/T^2 (T being the time it takes the object to complete one revolution) and the centripetal force.

I have yet to find the relationship of them though... I am having a bit of trouble comprehending it.

 

[Doc Al]

Start with the basic formula for centripetal force in terms of angular speed and radius. Look it up! (Given angular speed and radius, you should be able to calculate the period.)

 

[lord_blurg]

I can understand how the centripetal force can relate to the period. (Without the radius and velocity there would be no centripetal force acting)

The thing I am finding hard to comprehend is why we need 1/T^2? Why make a graph of 1/T^2 against Force when it is just as simple to create T against Force graph which is accurate.

Why turn it into a curved graph... do they look prettier lol.

Unless of course the curvature of the graph relates to the velocity and radius. I just don't see how it could though.

 

[Doc Al]

I can understand how the centripetal force can relate to the period. (Without the radius and velocity there would be no centripetal force acting)

Express this relationship mathematically. Start with the formula for centripetal force in terms of angular speed and radius.

The thing I am finding hard to comprehend is why we need 1/T^2? Why make a graph of 1/T^2 against Force when it is just as simple to create T against Force graph which is accurate.

The reason you would graph Force versus 1/T^2, instead of T or 1/T, will become clear when you find the relationship between centripetal force and period.

Why turn it into a curved graph... do they look prettier lol.

Actually, plotting F versus T would give you a more complicated, curved path. F versus 1/T^2 gives a much simpler curve.

 

[lord_blurg]

Thankyou for the help... I am starting to get it now.

I will keep you informed of how well I did with the practical.

 

[stoof]

i have a problem very similar to this one, with the same setup. However, the plug is supposed to represent a plantet's motion around the sun, with the string's tension represesenting the gravitational force between the planet and the sun. We have been told to investigate the relationship between its period and its radius, which i understand, but also what a change in planetary mass will cause. How would i best do this, by adding weight to the plug, or to the bag? and why?

 

[lord_blurg]

You must be doing gravitational fields =p...

I am up to that as well in my course.

When they are referring to the planetary mass (Often reffered to as M) they are talking about the mass which is exerting the main centripetal force. (i.e. the mass which is being revolved around.) If more mass is added to that then you will find that a larger force will be exerted to the plug due to more tension in the string. (I.e. the gravitational force) You will also find that for per unit of Mass there is also a unit of force due to them both being directly proportional.

With the radius... If you decrease the radius (r) then you will find that the period (T) will be smaller. Therefore there must be some kind of relationship between the radius and the period. (i.e. T is directly proportional to r)

Before you get all excited and start copying everything I said may I suggest that this stuff is only based on what I know (Which isn't very much) Don't take it litterally. It would be appreciated if some physics wiz commented on my help though. I am not even 100% sure if what I said is correct. :rofl: