Centroid of homogeneous lamina region R and the factor of "1/2"

[PainterGuy]

TL;DR

I found the formulas in two different sources for y-coordinate of center of gravity for a homogeneous lamina differ from each other by a factor "1/2".

Hi,

In one of the standard calculus textbooks, source #1, the formula for y-coordinate of center of gravity for a homogeneous lamina is given as follows.

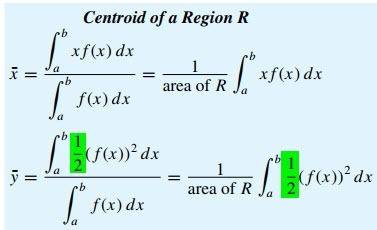
In another book of formulas, source #2, the formula is given without the factor "1/2" as is shown below. Personally, I believe that source #1 is correct. I just wanted to confirm so that I could notify the publisher of source #2 of erratum. Could you please help me with it? Thank you!

 

[PainterGuy]

Hi,

Could someone please comment on it? Thank you!

 

[pasmith]

If you start with the area integral for the centroid of the region bounded by x = a, x = b, y = 0 and y = f(x) you get <br /> \bar y = \frac{\int_A y\,dA}{\int_A\,dA} = \frac{\int_a^b \int_0^{f(x)} y\,dy\,dx}{\int_a^b \int_0^{f(x)}\,dy\,dx} = \frac{\int_a^b \left[ \frac12 y^2 \right]_0^{f(x)}\,dx}{\int_a^b \left[y\right]_0^{f(x)}\,dx}<br /> = \frac{\int_a^b \frac12 (f(x))^2\,dx}{\int_a^b f(x)\,dx} as stated.

 

[PainterGuy]

Thank you!

So, the factor of "1/2" should be there. I will let the publisher of source #2 that there is an erratum. Thanks.

 

[pasmith]

Thank you!

So, the factor of "1/2" should be there. I will let the publisher of source #2 that there is an erratum. Thanks.

The formula given in source #2 is the correct formula: by definition \bar y = \frac1A \int_A y\,dA.

The error in source #2 is not adequately explaining how to calculate it. It's only a coincidence that setting dA = f(x)\,dx gives the correct answer for \int x\,dA; doing the same for \int y\,dA does indeed result in the answer being out by a factor of two. I don't think setting dA = g(y)\,dy assists; after all, what is g if f is not strictly monotonic?