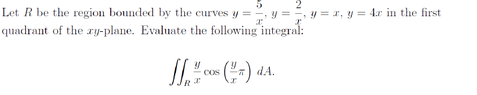Joe20
- 53
- 1
I have obtained as such using changing of variables/ transformations:
Let u= y/x and v= xy after manipulating the equation of the curves as such xy = 5, xy = 2, y/x = 1 and y/x = 4.
Then u = 1, u = 4, v = 5 and v = 2 => obtain a square on the u-v plane.
Change the integrand to:
Outer integral: 2 to 5
inner integral: 1 to 4
replace the expression for y/x to u [ u cos (u\pi) du dv]
I am not sure if I have done it correctly thus far. If so, how do i integrate that expression? Need advice.
Let u= y/x and v= xy after manipulating the equation of the curves as such xy = 5, xy = 2, y/x = 1 and y/x = 4.
Then u = 1, u = 4, v = 5 and v = 2 => obtain a square on the u-v plane.
Change the integrand to:
Outer integral: 2 to 5
inner integral: 1 to 4
replace the expression for y/x to u [ u cos (u\pi) du dv]
I am not sure if I have done it correctly thus far. If so, how do i integrate that expression? Need advice.