Characteristic Polynomials and Minimal polynomials

[xfunctionx]

Hi, there are a few questions and concepts I am struggling with. The first question comes in 3 parts. The second question is a proof.

Question 1: Please Click on the link below

Question 2: Please Click on the link below

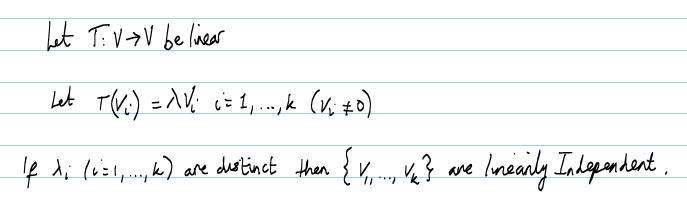
For Q2, could you please show me how to prove this. If possible, could you also link me to a web page where the full proof has already been provided?

I would appreciate the help.

 

[dx]

Hi xfunctionx,

Show us what you've done so far.

 

[xfunctionx]

sure ... let me just write it up

 

[xfunctionx]

Question 1 attempt: I got stuck early.

Question 2 attempt/proof from lecture notes:

I don't understand what my lecturer did right at the end. Or how his conclusion proved anything. Please could you help me understand, or show me a better proof?

 

[dx]

For question two:

You can prove this by induction. Clearly, it's true for k = 0 since eigenvectors are always non-zero. Now, to prove it for k = n, we assume it's true for k = n - 1.

Suppose that,

(a_1)(v_1) + (a_2)(v_2) + ... + (a_n)(v_n) = 0

Apply T to the LHS, and you get

(λ_1)(a_1)(v_1) + (λ_2)(a_2)(v_2) + ... + (λ_n)(a_n)(v_n) = 0

Now, multiply the first equation by λ_n, and subtract it from the second. The last term will cancel out. You will be left with

(λ_1 - λ_n)(a_1)(v_1) + (λ_2 - λ_n)(a_2)(v_2) + ... + (λ_(n-1) - λ_n)(a_(n-1))(v_(n-1)) = 0.

By the inductive hypothesis, each of the coefficients here must be zero. Can you show that this implies the the a_i from i=1 to (n-1) must be 0? (Hint: Use the fact that the eigenvalues are distinct). Then the original first equation becomes (a_n)(v_n) = 0, so a_n too must be zero.

 

[dx]

Clearly, it's true for k = 0 ...

Sorry, I meant k = 1.

 

[xfunctionx]

Sorry, I meant k = 1.

Thank you for your help dx, I will attempt the proof and try to understand it using induction.

 

[xfunctionx]

Can anyone help me with question 1?

 

[VKint]

Have you gone over the rational canonical form of a matrix? Or the Cayley-Hamilton theorem? If you have, question 1 should be straightforward. The answer to part (a) is yes (use the rational canonical form). For (b), use the Cayley-Hamilton theorem. For (c), write D = S^-1 T S, where S is an invertible matrix and D is diagonal. What's D²?

 

[mfarooq52003]

Hello xf...nx

Your proof of 2nd question which according to you is from Lecture notes is quite straight forward using definition of Linear independence and eigen vectors and the defined LT and given hypothesis of the theorem. It is the best and simplest proof you have. Just read a bit about Linear independence, eigen vectors and linear transformation and you will find that the proof is quite straight forward and simple.