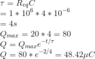Charge on the capacitor after changing the switch position

Click For Summary
SUMMARY

The discussion centers on analyzing the charging of a capacitor after changing the switch position in a circuit. When the switch is in position A, the voltage across the capacitor (Vc) is 0V due to prolonged connection, and the current (I) is calculated as 2 x 10^-5 A. Upon switching to position B, applying Kirchhoff's Voltage Law (KVL) yields a charge (Q) of 80μC on the capacitor, calculated using the formula Q = CV with C being 4 x 10^-6 F. The initial confusion regarding the time variable (t=2s) is clarified, confirming the calculations are correct without needing to reference time.

PREREQUISITES
  • Understanding of Kirchhoff's Voltage Law (KVL)
  • Familiarity with capacitor charging equations (Q = CV)
  • Basic knowledge of electric current and voltage relationships (V = IR)
  • Concept of steady-state conditions in electrical circuits
NEXT STEPS
  • Study the implications of time constants in RC circuits
  • Learn about transient analysis in capacitor circuits
  • Explore advanced applications of Kirchhoff's laws in complex circuits
  • Investigate the effects of varying capacitance on charge and voltage
USEFUL FOR

Students in electrical engineering, circuit designers, and anyone studying capacitor behavior in DC circuits will benefit from this discussion.

Fatima Hasan
Messages
315
Reaction score
14

Homework Statement


73_FFCE1_F-7820-4_D4_A-_BE3_F-_CAB58_E0_EED31.jpg


Homework Equations


V = I R
Q= CV

The Attempt at a Solution


When the switch is connected to position a :
20-106 * I = 0 ( KVL)
Vc = 0 , because the switch is connected for a long time.
I = 2*10-5 A
When the switch is connected to position b :
Q/(4*10-6) - 106 *2*10-5 = 0 (KVL)
Q =8*10-5 = 80μC
Is my answer correct ?
 

Attachments

  • 73_FFCE1_F-7820-4_D4_A-_BE3_F-_CAB58_E0_EED31.jpg
    73_FFCE1_F-7820-4_D4_A-_BE3_F-_CAB58_E0_EED31.jpg
    18.4 KB · Views: 698
Physics news on Phys.org
Fatima Hasan said:
Vc = 0 , because the switch is connected for a long time.
Are you sure?
Fatima Hasan said:
Is my answer correct ?
No, t=2s doesn't appear anywhere in your equations.
 
cnh1995 said:
Are you sure?

No, t=2s doesn't appear anywhere in your equations.
4%7D%20%3D%2048.png
 

Attachments

  • 4%7D%20%3D%2048.png
    4%7D%20%3D%2048.png
    2 KB · Views: 718

Similar threads

Electronic Circuits: Capacitors and switches
  • · Replies 11 ·
Replies
11
Views
2K
Finding Current in Resistors & Charge of Capacitor
  • · Replies 4 ·
Replies
4
Views
2K
Capacitor Questions Charging and Discharging
  • · Replies 4 ·
Replies
4
Views
4K
Find the unknown capacity of two capacitors
  • · Replies 5 ·
Replies
5
Views
2K
RLC Circuit Analysis -- Two sources and two switches
  • · Replies 3 ·
Replies
3
Views
2K
(LC Circuit) Finding cap charge after connecting to inductor
  • · Replies 18 ·
Replies
18
Views
5K
Two battery circuit charging one capacitor
  • · Replies 1 ·
Replies
1
Views
4K
Capacitors in a circuit with switches
  • · Replies 5 ·
Replies
5
Views
5K
Final Charge of a Capacitor in a Circuit with Capacitors and Resistors
  • · Replies 9 ·
Replies
9
Views
2K
Calculations involving different Dielectrics and Capacitors
  • · Replies 7 ·
Replies
7
Views
2K