Charges inside conducting sphere

[samjohnny]

Homework Statement

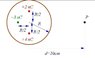
Three fixed point charges of +2 nC, −3 nC and +4 nC are located inside a thin uncharged metal spherical shell of radius R = 2 cm, as shown in the picture attached. Calculate the strength and direction of the electric field at position P, being 10 cm from the centre of the shell.

Homework Equations

E=Q/(4πε0r^2)

The Attempt at a Solution

I'm not sure what to do with this one. By Gauss' law the total enclosed charge of the metal sphere must be zero, but then how would one proceed with the question and calculate the field on P due to the charges in the sphere?

Thanks.

 

[BvU]

By Gauss' law the total enclosed charge of the metal sphere must be zero

How do you conclude that ?

 

[samjohnny]

How do you conclude that ?

Hmm, would it be correct to instead say in fact that inside the sphere, it is the electric field that is zero?

 

[BvU]

Same question. Don't you expect the field close to e.g. the -3 nC charge to be non-zero and point to that charge ?

 

[ehild]

Do not worry about the electric field inside the shell. You need it outside.

 

[BvU]

We were coming to that... gradually. The reply (no answer; instead: another question) to post #2 has me worried.

 

[samjohnny]

Same question. Don't you expect the field close to e.g. the -3 nC charge to be non-zero and point to that charge ?

I've had it drilled in my head that there is no electric field within a conductor and instead the charge migrates towards the surface [faraday cage and such]. I have probably mistakenly applied the result from that particular case to this situation as well. Yes, I would think that close to charge -3nC there is a non zero electric field due to it and pointing towards it.

 

[BvU]

What was drilled into your head is correct. But the conductor here is only the shell !

The three charges inside induce a surface charge on the inside of the shell, in such a way that the E-field is perpendicular to that inner surface. (Any component // the surface represents a non-zero E-field at the surface and would simply cause these charges to move until it's gone). The charge distribution on the inside surface is not asked for in this exercise (hence the EHild posting) .

Now, with the details of the surface charge distribution on the inside of the conducting shell of less interest, can you guess what the total charge on the inside of the shell must be ? (I could give a hint, but that's such a giveaway that it's your turn first).

From there, with the given neutrality of the shell, you have the total charge on the outside. Any idea how that charge is distributed ?

 

[samjohnny]

What was drilled into your head is correct. But the conductor here is only the shell !

The three charges inside induce a surface charge on the inside of the shell, in such a way that the E-field is perpendicular to that inner surface. (Any component // the surface represents a non-zero E-field at the surface and would simply cause these charges to move until it's gone). The charge distribution on the inside surface is not asked for in this exercise (hence the EHild posting) .

Now, with the details of the surface charge distribution on the inside of the conducting shell of less interest, can you guess what the total charge on the inside of the shell must be ? (I could give a hint, but that's such a giveaway that it's your turn first).

From there, with the given neutrality of the shell, you have the total charge on the outside. Any idea how that charge is distributed ?

Thanks for the reply. Ah I think I'm getting it, so it's only within the thin shell itself that the electric field is zero. As for within the hollowness of the sphere, there is a definite non zero charge and hence a non zero field there. I'm wondering if the total charge on the inside of the sphere would simply be negative of the sum of the three charges? And then the total charge on the outside will be equal to the sum of the three charges due to the shell being neutral but this will be uniformly distributed over the outer surface of the sphere since the shell itself, between the outer and the inner surface, conducts and so the electric field there is zero.

 

[BvU]

I'm wondering if the total charge on the inside of the sphere would simply be negative of the sum of the three charges?

Yes. No need to wonder: think a spherical Gaussian surface halfway between inner and outer surface of shell. E = 0 there !

And then the total charge on the outside will be equal to the sum of the three charges due to the shell being neutral but this will be uniformly distributed over the outer surface

Yes ! So this exercise ($\vec E$ at P) is a piece of cake !

In case you ever need to work out e.g. the charge distribution on the inner surface: "superposition principle" and "image charge" are the keywords (e.g. here).

 

[samjohnny]

Yes. No need to wonder: think a spherical Gaussian surface halfway between inner and outer surface of shell. E = 0 there !

Yes ! So this exercise ($\vec E$ at P) is a piece of cake !

In case you ever need to work out e.g. the charge distribution on the inner surface: "superposition principle" and "image charge" are the keywords (e.g. here).

Thanks for all the help! Here's what I've done (I think I might be grossly oversimplifying the physics; I'm just treating it as an electric field from a sphere/point charge problem):

E=Q/d^2*4*π*ε0 where Q = the sum of the charges = 3*10^[-9] C and d = 0.1m.

 

[BvU]

grossly oversimplifying

No, you're not. The effect of the conducting shell is indeed that the field outside is like that from a point net charge at the origin. (This is also the conlusion of A. Macchi (Pisa) in the link in post #10).

 

[samjohnny]

No, you're not. The effect of the conducting shell is indeed that the field outside is like that from a point net charge at the origin. (This is also the conlusion of A. Macchi (Pisa) in the link in post #10).

I see. Finally got my head around this, and have had a few misunderstandings cleared up. Thanks so much for the time and support!