phunphysics2
- 29
- 0
Greetings fellow Physics adorers,
I was wondering if someone could please check my work for this problem. I attached pictures of my work and the problem. It involves vectors.
My instructor said we will be having a problem like this on our exam, and it is an even problem so I'd definitely like to know if I am okay for this problem or not. Thanks for all the help!
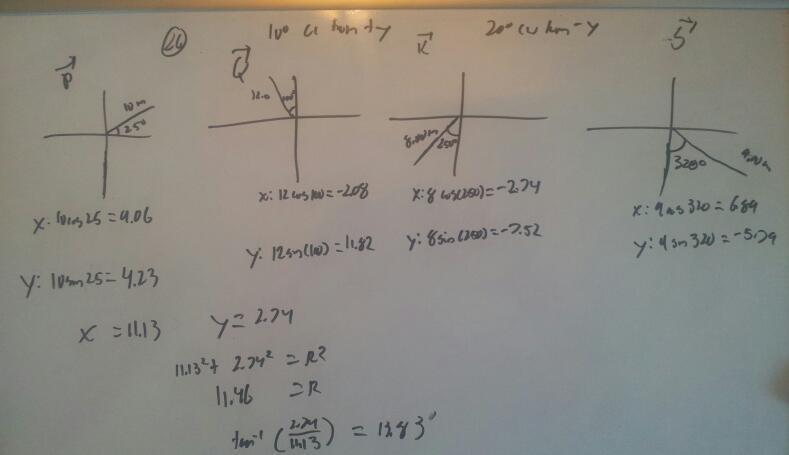

I was wondering if someone could please check my work for this problem. I attached pictures of my work and the problem. It involves vectors.
My instructor said we will be having a problem like this on our exam, and it is an even problem so I'd definitely like to know if I am okay for this problem or not. Thanks for all the help!