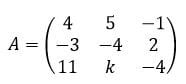Checking Invertibility of A^3 Matrix - Tips & Solutions

[Yankel]

Hi all,

I have the matrix A shown in the attached photo.

View attachment 3667

I need to check for which values of k, the matrix A^3 is invertible.

I tried calculating A^3, by multiplying A by itself twice. I got a nasty matrix. It makes no sense to me that now I am suppose to find it's rank, by using operations on rows. Am I missing something ? How would you solve this in the easiest way ?

Thanks !

 

[Euge]

Hi Yankel,

Note $A^3$ is invertible if and only if $A$ is invertible. How would you determine the values of $k$ that make $A$ invertible?

 

[Yankel]

Oh, I see, this was the missing part.

To find values for which A is invertible is easier. I find the rank of A, right ?

 

[Euge]

No, finding the rank of $A$ is unnecessary. If you can use determinants, find the values of $k$ for which $\text{det}(A) \neq 0$. If you don't know determinants, then consider row reducing the augmented matrix $[A|I]$ to Gaussian form.

 

[blue_raver22]

Hello,

To check for invertibility of A^3, you can use the following steps:

1. Calculate A^3 by multiplying A by itself twice.
2. Use Gaussian elimination or row operations to reduce the matrix A^3 to row-echelon form.
3. Check the rank of the reduced A^3 matrix. If the rank is equal to the number of rows/columns, then A^3 is invertible.
4. If the rank is less than the number of rows/columns, then A^3 is not invertible.

Alternatively, you can use the determinant of A^3 to determine invertibility. If the determinant is non-zero, then A^3 is invertible. If the determinant is zero, then A^3 is not invertible.

I hope this helps. Let me know if you have any further questions.

Best,