Chladni plate with Neumann conditions

[Smollett]

Hi there,
I'm trying to simulate a vibrating plate with free edges.
If i consider a consider a plate with fixed edges, the eigenvectors of the matrix bellow (which repesents the Laplacien operator) with S as a nxn tridiagonal matrix with -4 on the diagonal and 1s on either side (making the following a n² by n² matrix representing a plate with n² points).

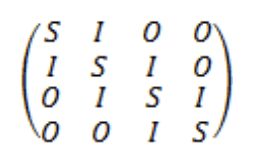
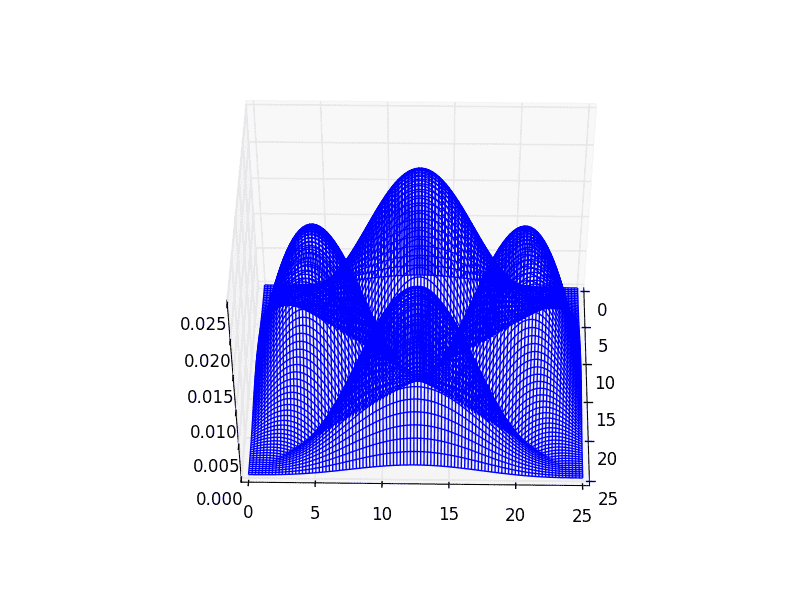
correspond to the state of the plate (the following example is for a plate simulated by a 4 by 4 grid), so i can generate the following images.

I found an article online (in french) which indicates that it is possible, using the same method but a different matrix to find the resonant states of a plate with free edges (Neumann conditions).
My only question is how to build a matrix with such conditions?

Has anyone encountered this problem before?

 

[Orodruin]

Think a bit about why the matrix looks the way it does. That should let you argue for how it changes.

 

[Smollett]

Thanks, I know why it looks that way, I made it.