Analyzing Forces in Circular Motion: Finding Equilibrium in a Spring System

[LCSphysicist]

Homework Statement

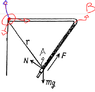
A device (Fig. 1.26) consists of a smooth L-shaped rod located in a horizontal plane and a sleeve A of mass m attached by a weightless spring to a point B. The spring stiffness is equal to x. The whole system rotates with a constant angular velocity co about a vertical axis passing through the point 0. Find the elongation of the spring. How is the result affected by the rotation direction?

Relevant Equations

N,
P = mg
F = minus kx

https://www.physicsforums.com/attachments/262043I got here, i think that the component y N will balance the mg force; the other componente of N will be divided in two, one to balance the force, and other to be the centripal result, but i don't know how relate to each other

 

[phinds]

your image is not visible.

 

[LCSphysicist]

 

[archaic]

Since this is a rotational motion with constant speed, what can you say about the tangential and centripetal accelerations (and thus the forces)?

 

[kuruman]

It would help if the figure showed points O, A and B mentioned in the statement of the problem. I can imagine the sleeve being the white cylinder labeled mg. Is the spring the black thing next to it? I would assume the axis of rotation is the black line on the left. If so, it is shown correctly parallel to the weight. Please show your attempt at this. When you do so and to avoid unnecessary confusion and utter chaos, please use $k$ not $x$ to denote the spring constant.

 

[wrobel]

nothing to understand

 

[LCSphysicist]

Since this is a rotational motion with constant speed, what can you say about the tangential and centripetal accelerations (and thus the forces)?

The tangencial force will cancel and the modulus of centripetal force will be constant since R is constant. ?
I don't know how to put this in a system possible and determined, that is, obtain the answer only with the variables given.

It would help if the figure showed points O, A and B mentioned in the statement of the problem. I can imagine the sleeve being the white cylinder labeled mg. Is the spring the black thing next to it? I would assume the axis of rotation is the black line on the left. If so, it is shown correctly parallel to the weight. Please show your attempt at this. When you do so and to avoid unnecessary confusion and utter chaos, please use $k$ not $x$ to denote the spring constant.

I totally agree with you

The blue axis is where route around.

I call B the point where the spring is attached

 

[haruspex]

View attachment 262047

The text says the L is in a horizontal plane. If so, what has mg to do with it?
The diagram is a perspective drawing, yes? The angle in the rod is really a right angle and the axis of rotation and the weight mg are normal to the L.
r is the hypotenuse... it's not clear, but I would guess the arms of the L are equal in length.

 

[kuruman]

The tangencial force will cancel and the modulus of centripetal force will be constant since R is constant. ?
I don't know how to put this in a system possible and determined, that is, obtain the answer only with the variables given.
I totally agree with you

View attachment 262053The blue axis is where route around.

I call B the point where the spring is attached

How about drawing a free body diagram of the sleeve showing all the hotizontal forces acting on it?

 

[LCSphysicist]

How about drawing a free body diagram of the sleeve showing all the hotizontal forces acting on it?

The problem is that just one force is on a horizontal, the elastic force. Look my justification:

Probably i am seeing wrong, this leave me to a lot components of N :|

 

[kuruman]

Are you saying that the rod does not exert a horizontal force? It will if it is necessary that it does so. In what direction is the centripetal acceleration? Can the elastic force account for all it? Hint: If the sleeve were at the end of a rod shaped like an I not like an L, that would be the case.

 

[archaic]

The tangencial force will cancel and the modulus of centripetal force will be constant since R is constant. ?
I don't know how to put this in a system possible and determined, that is, obtain the answer only with the variables given.
I totally agree with you

View attachment 262053The blue axis is where route around.

I call B the point where the spring is attached

the tangential components should be along the line perpendicular to the radius. suppose that there is an angle between the radius and the rod and project your forces onto it.