Time period of SHM & Energy conservation in pulley-spring-block system

[Aurelius120]

TL;DR Summary: I was solving this problem given in a book. The answer I got was wrong and seems to violate the conservation of mechanical energy. Yet the forces were balanced. Can someone provide an explanation.

So here is the problem:

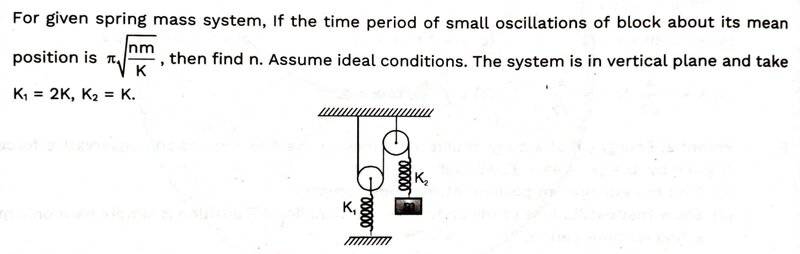
In the above arrangement, I had to find the time period . For right spring, $K_2=K$ and left spring, $K_1=2K$

In equilibrium,
$$T=K_2x=Kx=mg$$
$$2T=K_1y=2Ky=2mg \implies x=y$$(because of movable pulley)

Here is the problem.
For slow release of block (no change in KE), loss in PE of block is stored as PE of springs.
Because of movable pulley, thread moves by $2y$ and right spring extends $x$. Therefore block moves down by $(2y+x)=3x=3y$
By Conservation Of Energy,
$$mg(3x)=\frac{K_1y^2}{2}+\frac{K_2x^2}{2}$$
From my force balance equations above,
$$mg(3x)=\frac{2mgy}{2}+\frac{mgx}{2}=mgx+\frac{mgx}{2}$$(x=y)

This is not true and apparently violates the conservation of energy. So what happened to the rest of the energy if release was slow without change in kinetic energy.

What did I do wrong?

Ignoring the above violation I proceeded to as:
Since extension is both springs is equal, they can be treated as parallel combination of springs. $K_{net}=K_1+K_2=3K$
Then time period is $$2\pi \sqrt{\frac{m}{3K}}=\pi \sqrt{\frac{nm}{K}}$$ then $n=\frac{4}{3}$ which is different from the correct answer:$n=12$ Now this was rather expected as energy conservation was violated.

So how do I reach the correct answer?

 

[Aurelius120]

Just a clear diagram of the question

 

[kuruman]

By Conservation Of Energy,
$$mg(3x)=\frac{K_1y^2}{2}+\frac{K_2x^2}{2}$$

Why is this conservation of energy? Conservation of energy says$$\Delta K+\Delta U=0.$$ What happened to $\Delta K$? When you do the "slow release" bit, the hand that does the lowering performs non-conservative work on the mass that you have ignored.

Apply your "energy conservation" method to the simpler system of a mass hanging vertically from a single spring and see how that works.

 

[Aurelius120]

@kuruman That solves the energy conservation part. What about obtaining the correct solution? Since the conservation problem is resolved

For right spring, $K_2=K$ and left spring, $K_1=2K$

In equilibrium,
$$T=K_2x=Kx=mg$$
$$2T=K_1y=2Ky=2mg \implies x=y$$(because of movable pulley)
I proceeded to as:
Since extension is both springs is equal, they can be treated as parallel combination of springs. $K_{net}=K_1+K_2=3K$
Then time period is $$2\pi \sqrt{\frac{m}{3K}}=\pi \sqrt{\frac{nm}{K}}$$ then $n=\frac{4}{3}$ which is different from the correct answer:$n=12$

So how do I reach the correct answer?

What's wrong with this? Why do I get $4/3$ in place of $12$?

 

[nasu]

When you pull the block from equilibrium by some amount $\Delta z$, this is not equal to the extension of any of the two springs. You need to find the relationship between the restoring force (which is the increase in tension due to the displacement $\Delta z$) and the displacement of the block ($\Delta z$). The proportionality constant will be the effective spring constant for the SHO motion. The two springs do not act as two springs in parallel. And they don'textend by the same amount when you move the block from equilibrium.

 

[Aurelius120]

When I pull the block slowly by say $dF=Kdz$, it pulls the spring by $dz$ and the increase in tension $dT=Kdz$ which leads to extra $2dT$ on the other spring.
Therefore, $$2Kdz=2dT$$ so extension is equal, Right?

When you pull the block from equilibrium by some amount $\Delta z$, this is not equal to the extension of any of the two springs. You need to find the relationship between the restoring force (which is the increase in tension due to the displacement $\Delta z$) and the displacement of the block ($\Delta z$). The proportionality constant will be the effective spring constant for the SHO motion. The two springs do not act as two springs in parallel. And they don'textend by the same amount when you move the block from equilibrium.

 

[kuruman]

When I pull the block slowly by say $dF=Kdz$, it pulls the spring by $dz$ and the increase in tension $dT=Kdz$ which leads to extra $2dT$ on the other spring.
Therefore, $$2Kdz=2dT$$ so extension is equal, Right?

Right. The extensions are not the same in general, but they are so here. I was getting ready to post about this but you did so before me. I too get $n=\frac{4}{3}$. Do you have details of the "correct" solution?

 

[Aurelius120]

Unfortunately no details. That question has an answer on the internet that agrees with the book without any details.

Right. The extensions are not the same in general, but they are so here. I was getting ready to post about this but you did so before me. I too get $n=\frac{4}{3}$. Do you have details of the "correct" solution?

 

[nasu]

When you pull the bottom of the spring by some distance, the top of the spring does not move by the same distance. If it were so, the spring force won't change at all. It is the displacement of the top of the spring which is related to the displacement of the left pulley and not the displacement of the block. You need to relate the displacement of the block from equilibrium to the extra extensions of the two springs
The extra potential energy of the right spring depends on the difference between the displacements of the two ends.

 

[kuruman]

You need to relate the displacement of the block from equilibrium to the extra extensions of the two springs.

That's it. Define $x_1$ and $x_2$ as the displacements from equilibrium of left and right springs respectively. If the displacement of the mass from equilibrium is $x$, you have already established the constraint that $x=x_2+2x_1.$

 

[haruspex]

That's it. Define $x_1$ and $x_2$ as the displacements from equilibrium of left and right springs respectively. If the displacement of the mass from equilibrium is $x$, you have already established the constraint that $x=x_2+2x_1.$

Seems to me all that was done in post #1, but using x and y.
The error in post #4, as @nasu notes, is presuming these springs to be acting as in parallel merely because their extensions will match. Two identical ideal springs in series will also undergo equal extensions.
If we were to hold the block still and pull down on the left pulley, the left spring would shrink and the right spring would stretch. That is a series behaviour, not a parallel one.

Algebraically, if the mass exerts pull T on the RH spring then that expands by T/K, and the LH spring also expands by T/K, leading to a mass displacement of 3T/K. So, @Aurelius120, what is the effective spring constant?

 

[Aurelius120]

@haruspex
Then $$F_{net}=2K×\frac{T}{K}-K×\frac{T}{K}=K_{net}×3\frac{T}{K}$$$$ \implies K_{net}=\frac{K}{3}$$
Correct?
But how do we get that extension are equal on both strings from the constraint equation OR why is the spring combination a series one and not a parallel one?

Finally ,
Are these force equations correct for block moving down equilibrium position to lower extreme:

Constraint equation:$x=x_2+2x_1$
Double differentiating: $a=a_2+2a_1$
$k_2x_2=ma$ (net force on block below equilibrium)
$k_2x_2-T=m(2a_1)$ (thread pulled downwards by RH spring)
$2T-k_1x_1=ma_1$ (LH spring pulled above equilibrium)

If these are incorrect, what will be the correct force equations?

 

[kuruman]

@haruspex
Then $$F_{net}=2K×\frac{T}{K}\color{red}-\color{black}K×\frac{T}{K}=K_{net}×3\frac{T}{K}$$$$ \implies K_{net}=\frac{K}{3}$$
Correct?

Why the minus sign?
The sign set aside, the equation does not make sense. After correcting the sign, I get
$$F_{net}=2\cancel{K}×\frac{T}{\cancel{K}}+\cancel{K}×\frac{T}{\cancel{K}}= 3T.$$ Where did $K_{net}$ come from? It looks like you put down what will give you the answer $n=12$ without justification.

Actually, you are replacing the springs with an "effective" not net, spring constant $K_{e\!f\!f}.$ Labeling set aside, you have the equation $x=x_2+2x_1$. You want to replace the two springs with a single spring hanging from a string so that, when the mass is displaced by $x$, the effective spring will produce an elastic force that is equal to the net force on the mass in the actual two-spring case.

So you rewrite this equation replacing $x_1$ and $x_2$ as ratios of the tension over the spring constant. $$x=2\times\frac{2T}{K_1}+\frac{T}{K_2}.$$ Then you do some algebra to isolate $T$on the LHS to get $$T=\left(\frac{\text{Numerator}}{\text{Denominator}}\right)x.$$ For a single effective spring, the term in parentheses is the constant of proportionality between the net force on the mass and the overall displacement of the mass. This term then is $K_{e\!f\!f}.$

Do you see where to go from here?

 

[Aurelius120]

Why the minus sign?
The sign set aside, the equation does not make sense. After correcting the sign, I get
$$F_{net}=2\cancel{K}×\frac{T}{\cancel{K}}+\cancel{K}×\frac{T}{\cancel{K}}= 3T.$$ Where did $K_{net}$ come from? It looks like you put down what will give you the answer $n=12$ without justification.

Actually, you are replacing the springs with an "effective" not net, spring constant $K_{e\!f\!f}.$ Labeling set aside, you have the equation $x=x_2+2x_1$. You want to replace the two springs with a single spring hanging from a string so that, when the mass is displaced by $x$, the effective spring will produce an elastic force that is equal to the net force on the mass in the actual two-spring case.

Ok thanks. I don't know why I thought directions of force due to LH spring will oppose RH spring and therefore the minus.

So you rewrite this equation replacing $x_1$ and $x_2$ as ratios of the tension over the spring constant. $$x=2\times\frac{2T}{K_1}+\frac{T}{K_2}.$$ Then you do some algebra to isolate $T$on the LHS to get $$T=\left(\frac{\text{Numerator}}{\text{Denominator}}\right)x.$$ For a single effective spring, the term in parentheses is the constant of proportionality between the net force on the mass and the overall displacement of the mass. This term then is $K_{e\!f\!f}.$

Do you see where to go from here?

Yep .
$$x=2\times\frac{2T}{K_1}+\frac{T}{K_2}.=2\times \frac{2T}{2K}+\frac{T}{K}$$$$\implies x=\frac{3T}{K}\implies T=\frac{K}{3}x$$
My sleep will be peaceful tonight

 

[Aurelius120]

So that problem is resolved. But if $T=K_2x_2$ and $2T=K_1x_1$
Constraint equation:$x=x_2+2x_1$
Double differentiating: $a=a_2+2a_1$
Then acceleration of block should be zero? If there is no force difference between $T$and $K_2x_2$, $2a_1$ should be zero? Similarly $a_2=0$

Constraint equation:$x=x_2+2x_1$
Double differentiating: $a=a_2+2a_1$
$k_2x_2=ma$ (net force on block below equilibrium)
$k_2x_2-T=m(2a_1)$ (thread pulled downwards by RH spring)
$2T-k_1x_1=ma_1$ (LH spring pulled above equilibrium)

If these are incorrect, what will be the correct force equations?

So are the force equations wrong.

 

[haruspex]

But how do we get that extension are equal on both strings from the constraint equation

It does not follow from a constraint equation; it follows from the happenstance that the spring with twice the spring constant is subject to double the string tension. If we were to introduce another mass between the springs there would be other modes of oscillation and the two spring extensions need no longer match.
The kinematic constraint is that the displacement of the mass equals the stretch of the one spring plus twice the stretch of the other.

why is the spring combination a series one and not a parallel one?

It is not purely either. It is more like series because, in principle, the springs could be stretched independently, each leading to a displacement of the mass. However, for the same magnitudes of stretch the two displacements are different, which is not so for springs in series.

 

[kuruman]

So are the force equations wrong.

Asking this question shows that you are still uncertain about what you are doing. There is only one force equation, the one that involves the effective spring constant. What is this equation and how will it help you find the period of small oscillations?

 

[nasu]

So that problem is resolved. But if $T=K_2x_2$ and $2T=K_1x_1$
Constraint equation:$x=x_2+2x_1$
Double differentiating: $a=a_2+2a_1$

What do you mean by $a_1$ and $a_2$? What objects have these acceleration? What is the meaning of the "mass" in what you call force equations for these accelerations?

 

[Aurelius120]

What do you mean by $a_1$ and $a_2$? What objects have these acceleration?

They are the acceleration due to each spring. Since $x_1$ and $x_2$ are spring extensions and $x$ is block displacement
Double differentiating should give their accelerations.

What is the meaning of the "mass" in what you call force equations for these accelerations?

I forgot these springs and pulleys were massless and that they could have different accelerations without any difference in force between them.
So I $2ma_1=k_2x_2-T$ was force on string due to RH spring and all those other equations.

Needless to say, thats what had been holding me back from the correct answer despite all provided explanations.

 

[nasu]

Within the simpified model used in the problem, the only objet with mass is the block. There is only one instance of Newton's second law for the system, the one for the block. All the other equations result from the constraints and the Hooke's law for the two springs.

 

[kuruman]

Needless to say, thats what had been holding me back from the correct answer despite all provided explanations.

Please answer my questions in post #17. Then you will see where this is going.

 

[Aurelius120]

What is this equation and how will it help you find the period of small oscillations?

$$K_{eq}x= K_2x_2=T \ \ and \ \ K_1x_1=2T$$
Once $K_{eq}$ is found, $\omega = \sqrt{\frac{K_{eq}}{m}}$
Then $time=\frac{2\pi}{\omega}$

 

[kuruman]

You are halfway there. What is the period that you called $time$ in terms of $K_{eq}$?

 

[Aurelius120]

Time
$$=2\pi\sqrt{\frac{m}{K_{eq}}}=2\pi\sqrt{\frac{3m}{K}}=\pi\sqrt{\frac{nm}{K}} \implies n=12$$

 

[kuruman]

Time
$$=2\pi\sqrt{\frac{m}{K_{eq}}}=2\pi\sqrt{\frac{3m}{K}}=\pi\sqrt{\frac{nm}{K}} \implies n=12$$

Good job.