Xari
- 3
- 0
Thread moved from the technical forums, so no HH Template is shown.
I'm having trouble solving this problem. I did Google the solution with the steps, which I managed to actually get right in all aspects except for a small part in the trigonometry that throws me off.
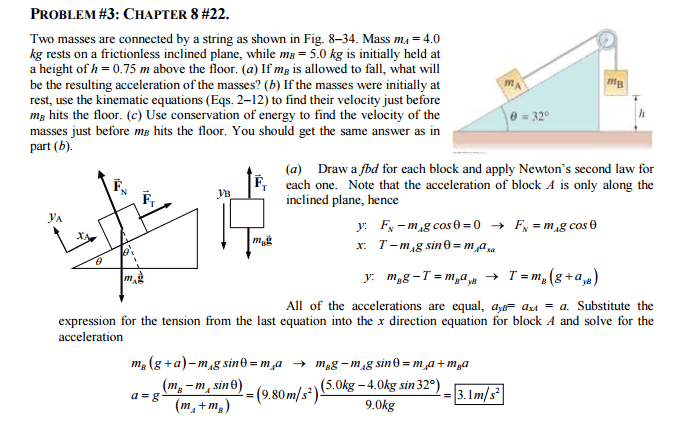
I drew my FBD's correctly, hopefully. I'm not sure how I can draw nice looking FBDs online, but here goes.
In the solution it says that the acceleration of mass A is mg * sin (theta). Why is that so? I thought that we're trying to get gravity's force on the object with the formula: sin (theta) = (mA * g) / hypotenuse ----------->
hypotenuse = (mA * g) / sin (theta). That way we'd get the force in the direction opposite to the force of tension, which is caused by mB * g?
If I'm not wrong, isn't sin (theta = opp / hypotenuse? How did they get sin (theta) * mAg when that isn't even feasible in the trigonometry equation of sin(theta) = (mAg)/hypotenuse?
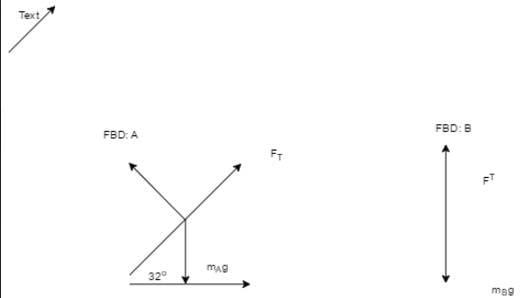
I drew my FBD's correctly, hopefully. I'm not sure how I can draw nice looking FBDs online, but here goes.
In the solution it says that the acceleration of mass A is mg * sin (theta). Why is that so? I thought that we're trying to get gravity's force on the object with the formula: sin (theta) = (mA * g) / hypotenuse ----------->
hypotenuse = (mA * g) / sin (theta). That way we'd get the force in the direction opposite to the force of tension, which is caused by mB * g?
If I'm not wrong, isn't sin (theta = opp / hypotenuse? How did they get sin (theta) * mAg when that isn't even feasible in the trigonometry equation of sin(theta) = (mAg)/hypotenuse?
