Classify the given second-order linear PDE

[chwala]

Homework Statement

Classify the second order linear pde, given by;

$U_t +2U_{tt}+3U_{xx}=0$

Relevant Equations

use of discriminant

Now i learned how to use discriminant i.e $b^2-4ac$ and in using this we have;
$b^2-4ac$=$0-(4×3×2)$=$-24<0,$ therefore elliptic.

The textbook has a slight different approach, which i am not familiar with as i was trained to use the discriminant at my undergraduate studies...
see textbook approach here;

and the textbook solution is here;

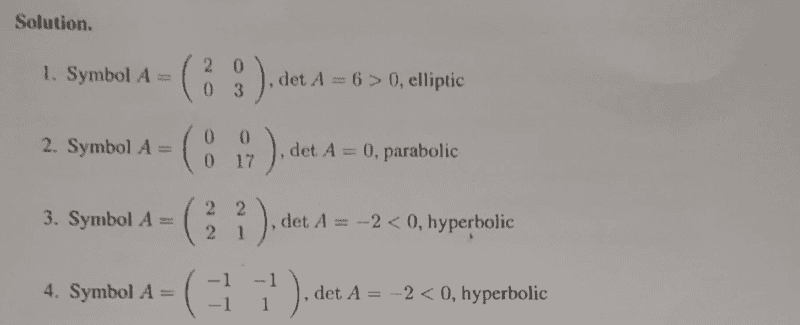and i also checked wikipedia on this and they have used the discriminant approach. See the approach here; ( i am comfortable with this approach)

Both approaches should be fine, one can use either approach...correct?

 

[Office_Shredder]

The textbook is the same thing with some math modifications

1.) Instead of $b^2-4ac$ they have $4ac-b^2$ so the sign is flipped

2.) They write $2b$ as the coefficient instead of $b$. So given that the coefficient of the cross term is called $2b$, their discriminant becomes
$4ac-(2b)^2=4(ac-b^2)$. Since 4 is positive, the sign of the discriminant is determined by $ac-b^2$.

 

[chwala]

The textbook is the same thing with some math modifications

1.) Instead of $b^2-4ac$ they have $4ac-b^2$ so the sign is flipped

2.) They write $2b$ as the coefficient instead of $b$. So given that the coefficient of the cross term is called $2b$, their discriminant becomes
$4ac-(2b)^2=4(ac-b^2)$. Since 4 is positive, the sign of the discriminant is determined by $ac-b^2$.

ooooh, Thanks am trying to refresh on pde's cheers mate...