COG calculation of diffracted spots on a camera

[Gifty01]

TL;DR Summary

COG calculation of diffracted spots on a camera

Hi all,

I will like to simulate diffracted spots at least two spots, on a camera. I will be glad if someone can help out with a code. below are the details required:
camera pixel size = 4um (each pixel can be sub divided for better calculation), gap size = 100nm, camera length = 4000 x 4000 pixels, diffracted spot size on the camera = 30 um (airy disk eqn or gaussion eqn can be used to simulate the diffracted spot), photon noise = poisson distribution, read out noise = zero mean normal noise, monte-carlo simulation = 500 random realizations. Other details if needed are:
saturation capacity = 10300, QE = 68%, SNR =6.7 bit.

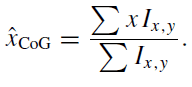Eqn for COG calculation

At each iterations, the true center is placed randomly within the CCD pixel and then compared to the measured center.

A graph of Center of gravity (COG) against spot positioning (i.e moved across the sensor from left to right) should be calculated. A sample of how the plot will look like is attached.

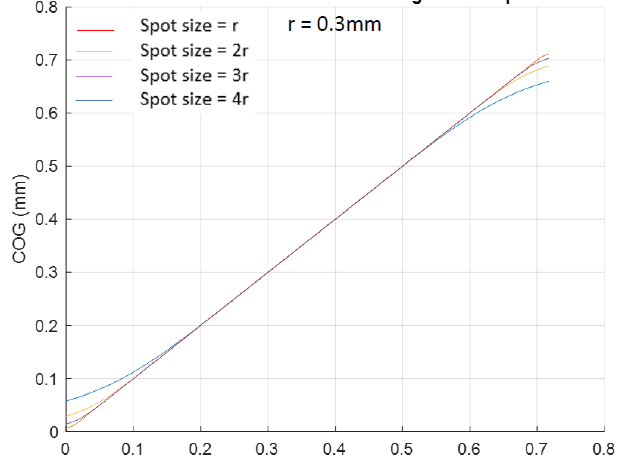
Due to effect of sensor edge, the COG calculation deflects from the real value. I will like to create a matrix which corrects the COG calculation by subtracting e.g at the left edge of the edge, and adding up e,g at the other edge to the right. since the measured COG value is known. Thanks in advance.

 

[sophiecentaur]

Summary:: COG calculation of diffracted spots on a camera

I will like to simulate diffracted spots at least two spots, on a camera.

Not quite sure what you mean. Is the diffraction pattern due to the diameter of the optics? If so, then the output of a sensor pixel will be a rectangular / square sample in 2D.

In terms of basic ideas on sampling theory. Just working on one dimension, for a start (imagining a long, narrow sensor element), the output level on the sensor pixel will be the integral of the diffraction pattern between the limits of the sensor width. If you were to scan the sensor across the image, you would get a low pass filtered (smoothed) version of the original pattern.

 

[Gifty01]

Thanks for your response sophiecentaur. The diffraction is due to the size of the aperture. I am not so good in coding. I wrote a bad code with MATLAB which takes a lot of time to run completely. the graph showing the plot of COG against spot position was the plot I obtained, which shows that there is much deviation of the spot position and the calculated COG, which is due to the finiteness of the pixel or sensor (since we used a finite sensor to sample a continuous function in this case the airy disk). That was why I am trying to obtain a matrix that could be added to effectively calculate the COG so as to get rid of the sensor edge effect. Thanks.

 

[sophiecentaur]

I am not so good in coding.

Practice makes perfect. It is ages since I did anything more than formulae in Excel.
Your problem could be straightforward - certainly it is in one dimension. That's just like the simple moments calculations.
if M is the total mass of a line of small masses m0 m1, m2 ...mn and they are spaced by d, the basic 'school' method to find the position x of M from one end of the row is:
M.x = d.m₁ + 2d.m₂ + 3d.m₃ + 4d.m₄ . . .etc . . .
In 2D, your m values would be the sum of the my 's on either side of the position of the max of the mx 's. It will give you a corrected x position for the CM to somewhere to one side of the chosen maximum. If you get several equal values of m, you can use the first and the correction will take care of it. In fact you can take any starting point but you wouldn't want to use too big a range or you could catch two stars.
If that makes sense then you can do the same for the y distances in the array.
There may be better approaches but I could code that without too much trouble
I just looked on Google and found this which does just what I said.