Combined tensions of an RLC series circuit with AC current

[Thai777]

Homework Statement

In the RLC circuit that follows, we have that R= 8$\Omega$, L= 40mH, C=20$\mu$F. The source maximal tension is $\Delta v_0$ = 100 V and the frequency is f=200/$\pi$ Hz.
Find the maximum tensions between the terminals of a) R, C and L independently; b) R and C combined; c) C and L combined.

Relevant Equations

$Z = \sqrt{R^2+(Z_L - Z_C)^2}$
$\Delta v = i Z$

This is an exercise from Harris Benson Electricity book 2nd edition ch12 P12 if anyone want to see it. I've taken the liberty to translate it from french to english.
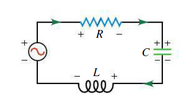
The circuit in question is simply a RLC serie circuit in the order of AC source -> Resistor -> Capacitor -> Inductor -> back to AC source.


I have used the equation $$\begin{align} Z = \sqrt{R^2+(Z_L - Z_C)^2}\end{align}$$
to find the total impedance and then used the following equations
$$\begin{align} \Delta v_0 = i_0*Z \\
\Delta v_{R0} = i_0*R \\
\Delta v_{C0} = i_0*Z_C \\
\Delta v_{L0} = i_0*Z_L \\
\end{align}$$
To find each max tensions.
I find respectively, $\Delta v_{R0} = 7.36V$, $\Delta v_{C0} = 115V$ and $\Delta v_{L0}=14.7V$.

So far so good, I am just a bit confused about the answers of b) and c).
From my understanding of the book, when you want to combine tensions in AC circuits, the phase differences make it trickier because the actuals values are oscillating in time and are therefore best represented with vectors in complex space (phasors).
Therefore you need to do a vector sum and then find the norm of that final vector.
Thankfully, in this very simple circuits every component are either $\pi/2$ phase shifted or just in phase which makes them all easy to compute.

I believe, the current $i(t)$ and the tension of the resistor $\Delta v_R(t)$ are in phases, the inductor tension $\Delta v_L(t)$ and capacitor tension $\Delta v_C(t)$ are both respectfully early and delayed by $\pi/2$.

Therefore for b), if we assume that the resistor tension $\Delta v_R(t=0)$ is completely in the real axis, the capacitor $\Delta v_C(t=0)$ is completely in the negative imaginary axis and the vector sum is simple and we can use pythagorean theorem to find the tension sum
$$\begin{align} \|\Delta v_{RC}\| = \sqrt{\Delta v_{R0}^2 + \Delta v_{C0}^2}
\end{align}$$
Which gives me 115V.

For c), I assume the same thing as b), but this time the inductor $\Delta v_L(t=0)$ is completely in the imaginary positive axis, and therefore we can simply do a sum to find the final vector norm.
$$\begin{align} \|\Delta v_{CL}\| = |\Delta v_{C0} + \Delta v_{L0}|
\end{align}$$
Where I took $\Delta v_{C0} = -115V$ and $\Delta v_{L0} = +14.72V$
Therefore it gives me 100V.

My question is simple, why is it that in the answer at the end of the book, they write that the answer of c) is -100V? What exactly is the signification of this negative? Why is the answer in b) not negative either then (the answer in b is +115V) ?

I woud like to see if I did any errors or if someone could elucidate me in the reasoning of the negative sign.

Thank you!

 

[DaveE]

I find respectively, ΔvR0=7.36V, ΔvC0=115V and ΔvL0=14.7V.

Yes, close enough. I found 7.320V, 114.371V, 14.640V. Note that these are the magnitudes. They have a phase shift that you have to work with for the other questions.

if someone could elucidate me in the reasoning of the negative sign.

Are you familiar with the use of complex numbers (phasors, really) and their arithmetic?
If I wrote $Z(\omega) = R + j \omega L + \frac{1}{j \omega C}$ would you be able to find it's magnitude?
This is, for me, the easiest way to see where the negative sign comes from in your formula for $|Z|$. That negative sign results from the fact that the voltages of L and C are 180^o out of phase, so you subtract their magnitudes when they are summed in series.

$Z(\omega) = R + j \omega L + \frac{1}{j \omega C} = R + j (\omega L - \frac{1}{ \omega C})$

$|Z(\omega)| = \sqrt{ R^2 + (\omega L - \frac{1}{ \omega C})^2 }$

 

[Thai777]

Yes, close enough. I found 7.320V, 114.371V, 14.640V. Note that these are the magnitudes. They have a phase shift that you have to work with for the other questions.


Are you familiar with the use of complex numbers (phasors, really) and their arithmetic?
If I wrote $Z(\omega) = R + j \omega L + \frac{1}{j \omega C}$ would you be able to find it's magnitude?
This is, for me, the easiest way to see where the negative sign comes from in your formula for $|Z|$. That negative sign results from the fact that the voltages of L and C are 180^o out of phase, so you subtract their magnitudes when they are summed in series.

$Z(\omega) = R + j \omega L + \frac{1}{j \omega C} = R + j (\omega L - \frac{1}{ \omega C})$

$|Z(\omega)| = \sqrt{ R^2 + (\omega L - \frac{1}{ \omega C})^2 }$

Yes, I am familiar with complex number and can do arithmetic with it. It's just that the book doesn't go at all into it so I don't know how it would be formally written in RLC circuits.

I've given a try, and I get something very different, please correct me or show me how it should be done!

Using the equation
$|Z| = \sqrt{ R^2 + (\omega L - \frac{1}{ \omega C})^2 }$
I rewrite it as
$$\begin{align} i_0|Z| = \sqrt{i_0^2 R^2 + (i_0 Z_L - i_0 Z_C)^2} \\
|\Delta V| = \sqrt{\Delta v_{R0}^2 + (\Delta v_{L0}-\Delta v_{C0})^2}
\end{align}$$
Where I used the relation $\Delta v_{k0} =Z_{k} i_0$ Where $Z_{k}$ for the resistor is $R$. I assume the problem is asking for $|\Delta V|$ that I have written since it is the norm of the tension vector.

Now I will assume that the tensions $\Delta v_{k0}$ with k={R, L, C} can be written as
$\Delta v_{k0} = |\Delta v_{k0}|e^{j(\omega t+\phi_k)}$ where $j=\sqrt{-1}$.

I'm gonna assume t=0 and $\phi_k = {0, +\pi/2, -\pi/2}$.
We can therefore says that the phase for each component respectively are $e^{j(0)} = 0$, $e^{j(\pi/2)} = j$ and $e^{j(-\pi/2)} = -j$.

Now using the equation I derived previously and with $|\Delta v_{R0}| = 7.36V$, $|\Delta v_{L0}| = 14.7V$ and $|\Delta v_{R0}| = 115V$, I will look at question b) where we only care about the Resistor and Capacitor together. So, $Z_L = 0$ and $\Delta v_{L0} = 0$

$$\begin{align} \Delta V_{RC} = \sqrt{\Delta v_{R0}^2 + (0 -\Delta v_{C0})^2} \\
|\Delta V_{RC}| = \sqrt{|\Delta v_{R0}^2| + (-|\Delta v_{C0}|*-j)^2} \\
|\Delta V_{RC}| = \sqrt{7.36^2 + (115^2*j^2)} \\
|\Delta V_{RC}| = \sqrt{-13171} = 115j
\end{align} $$
This gives a complex number??

Now if I do a similar thing for c) and I set $R=0$ to look at LC only.
$$\begin{align} \Delta V_{RC} = \sqrt{0 + (\Delta v_{L0}^2 -\Delta v_{C0})^2} \\
|\Delta V_{RL}| = \sqrt{(|\Delta v_{L0}|j - |\Delta v_{C0}|*-j)^2} \\
|\Delta V_{RL}| = \sqrt{(129.7j)^2} \\
|\Delta V_{RL}| = 129.7j
\end{align} $$
This also give me a complex number! Now, I think I heard before that the square root is not well defined for complex number so maybe I just did bad math.

Elaborate on how you'd use complex number in the problem and why there would be a sign difference between the answer of b) and c) please!

 

[DaveE]

Sorry, I'm a bit too busy today to go through this in detail. I would strongly suggest you review AC circuits, complex impedances, and phasors. Khan Academy has some really good tutorials for this (in English).

But some general comments:

- Every quantity in an AC steady state circuit has a magnitude and phase. Every voltage and current. These can be represented as a complex number in polar form. Each also has a time varying factor of $e^{j \omega t}$ which can be factored out. Since that factor (multiplier) is always the same it is ignored or assumed to always be present. This is the genesis of phasor notation.

- One of the quantities will have a phase arbitrarily assigned to it. Phase only makes sense in relation to another wave form. Every phase is really a phase shift. Normally we choose the source applied to the network and give it a phase of zero.

- Impedances will convert complex valued voltages into complex valued currents, or vice-versa. They are also represented with a complex number which alters the magnitude and phase of the voltage or current. Impedances are constant and don't have the time varying factor of $e^{j \omega t}$.

- You can solve simple circuits with complex impedances the same way you would solve a DC circuit with only resistors. Except, you will be using complex numbers instead of real numbers. All of the tools you used, like KCL, KVL, voltage dividers, etc. also work with complex impedances and steady state AC voltages and currents. You just need to be more careful with the complex arithmetic.

- Keep all of your workings with complex numbers and don't calculate magnitudes or phases until the very end. This is because the phase will effect the magnitude when you are adding and subtracting things. So, your calculation of $i_o|Z|$ doesn't really make sense. You've kept the phase shift in $i_o$, but removed the phase shift from $Z$. It should be $V=i_oZ$, or $|V|=|i_oZ|=|i_o||Z|$.