- #1
EROC
- 4
- 0
Homework Statement
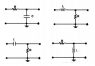
In each of the four circuits shown,
an AC input voltage, ##V_0 cos(\omega t)## is applied on the
left and the output voltage is measured on the
right. Treat the input frequency as a variable.
(a) For each case, state whether high or low
frequencies are passed or suppressed in the
output and explain your answer briefly.
(b) You have a 0.47 µF capacitor. Select the
circuit that allows high frequencies to pass.
Calculate the resistor value such that ##V_(out) / V_(in)## is
1/ sqrt(2) at 200 Hz. Such a filter could be used to reduce 60 Hz “hum” in an audio circuit. What is ##V_(out) / V_(in)## at 60 Hz?
(c) You have a 3 mH inductor. Select the circuit that allows high frequencies to pass. Calculate the
resistor value such that ##V_(out) / V_(in)## is 1/ sqrt(2) at 200 Hz. Optional: comment on whether you anticipate
any issues implementing this circuit with real components
**Cannot use high-pass / low-pass filters**
This is mainly an RLC circuit question in a basic physics: electrostatics and magnetism course, so it is focused on basic circuit ideas.
Homework Equations
##V=IZ##
##X_L = \omega L##
##X_C = 1 / (\omega C)##
The Attempt at a Solution
I don't know what I am supposed to be doing or observing for the first one. An upperclassman I know can explain it in circuit theory, but I do not know circuit theory and will not be learning it in this course.
Any help would be great, and an explanation please!