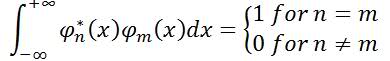Completeness of Eigenfunctions

[andyc10]

I understand what is meant by the orthogonalilty of eigenfunctions...

...but what is measnt by the completeness of eigenfunctions?

 

[D H]

In short, the eigenfunctions span the function space. Every function in the space can be represented as a linear combination of the eigenfunctions, and every Cauchy sequence of linear combinations of the eigenfunctions converges to an element of that space.

 

[Avodyne]

$$\sum_n \varphi_n(x)\varphi^*_n(y)=\delta(x-y)$$

 

[0xDEADBEEF]

The answer to this question is very subtle. Simply put completeness means, that you can produce any function of your space with a weighted sum of your base functions. But this requires you to know what space you are working in. Physicists use the "complete orthonormal base" to say that no information is lost, by expanding a state into other functions.

That was the part to clarify now comes the part to confuse...

Even one function can be the complete base of a very boring function space. But you would normally take an $$\mathrm{L}^2$$-Space I suppose, but there are more problems involved all of them very mathematical.
It is very seldomly shown that a base is indeed complete, and it is seldomly defined which space one is working in. I suppose the most powerful ones called "Gelfand triples" are still an area of active research.

 

[ice109]

$$\sum_n \varphi_n(x)\varphi^*_n(y)=\delta(x-y)$$

or 1 for the space he's talking about

 

[Hurkyl]

or 1 for the space he's talking about

I can't figure out how that could make sense.

(Did you overlook that there's both an x and a y on the l.h.s.?)

 

[George Jones]

I can't figure out how that could make sense.

(Did you overlook that there's both an x and a y on the l.h.s.?)

I think ice109 meant Dirac notation. Starting from completeness expressed using Dirac notation, and proceeding formally as in a quantum text (which you might hate) leads to completeness expressed in terms of wavefunctions, as given by Avodyne.

$$\begin{equation*} \begin{split} 1 &= \sum \left| \phi _{n}\right\rangle \left\langle \phi _{n}\right|\\ \left| y\right\rangle &= \sum \left| \phi _{n}\right\rangle \left\langle \phi _{n}|y\right\rangle\\ \left\langle x|y\right\rangle &= \sum \left\langle x|\phi _{n}\right\rangle \left\langle \phi _{n}|y\right\rangle\\ \delta \left( x-y\right) &= \sum \phi _{n}\left( x\right) \phi _{n}^{\ast }\left( y\right) \end{split} \end{equation*}$$

The initial post was phrased in terms of wavefunctions.

 

[Hurkyl]

I have no problem with the fact you can convert back and forth between the resolution of the identity and what Avodyne wrote -- I just had a problem with ice's assertion that what Avodyne wrote was supposed to have a 1 on the R.H.S.


I actually don't have a problem with your derivation; it's clearly meant to be distributional in the variables x and y, and the product $\langle x \mid y \rangle$ doesn't have the "multiplying distributions" problem.

It did give me pause, though, because I'm so unused to seeing distributions written "plainly" mixed with calculations done in Dirac notation.

i.e. I would have expected a calculation in Dirac notation to result in something that looked like $|x\rangle\langle y|$, which offers an unmatched ket and bra against which one can inner product away the distributional variables.

 

[ice109]

i take it back. i have to admit i don't understand what avodyne wrote, in fact i don't know how to interpret what he wrote because of the distribution on the right not being under an integral. though i was referring to the completeness identity in the first line of george's derivation.

i also don't understand the transition from the right hand side of the third line to the right hand side of the fourth line in george's post.

really what i actually meant is that if

$$\int_{-\infty}^{\infty}\phi_m^* \phi_n= \delta_{mn}$$

then the wavefunctions are truly orthonormal and not dirac orthonormal. but now i realize that that is completely besides the point.

 

[ExactlySolved]

It did give me pause, though, because I'm so unused to seeing distributions written "plainly" mixed with calculations done in Dirac notation.

i.e. I would have expected a calculation in Dirac notation to result in something that looked like $|x\rangle\langle y|$, which offers an unmatched ket and bra against which one can inner product away the distributional variables.

Hi Hurkyl, I am a physicist who knows enough math to appreciate why the plain mixing of dirac distribution concerns you, but I don't know enough to flesh out the details of your comment about $|x\rangle\langle y|$, I would be appreciative if you could say something more about this.

 

[Hurkyl]

Well, part of the problem you're having is probably that I haven't written something quite accurate. I knew something was bothering me, but i hadn't yet exactly pinned it down.

Basically, the point is that, using the tempered distribution definition, that $\delta(x - y)$ is the operator that takes a pair of test functions f and g and produces the number

$$\delta(x - y) \star (f(x), g(y)) := \int_{-\infty}^{+\infty} f(x) g(x) \, dx$$

(Of course, $\star$ is more usually written in integral notation)


In dirac notation, distributions can be written as bras or kets or other operators; for example, the operator T defined by $T(x) \star f(x) := f(0)$ would would be the bra $\langle 0 \mid$ (assuming we were writing our functions as kets).


And so, I wonder to myself why we are writing $\delta(x - y)$, rather than expressing this distribution as a ket or a bra or an operator of some sort... but alas I'm not seeing how to do the conversion. I think it's because both x and y are explicit variables, not hidden ones. Everything looks like it's fine, but I still feel somehow uncomfortable about it.

 

[nam]

Following is my explanation (pls respond if it is correct or not):

eigenfunctions $\phi_n(x)$ form a complete set => any function $f(x)$ can be uniquely and exactly expanded in terms of $\phi_n(x)$,
$$
f(x)=\sum_n c_n\phi_n(x) => c_n=\int f(x')\phi_n^*(x')dx'
$$
$$
=> f(x)=\sum_n \phi_n(x)\int f(x')\phi_n^*(x')dx'=\int dx'f(x')\sum_n \phi_n(x)\phi_n^*(x')
$$
Compare this with
$$
f(x)=\int dx'f(x')\delta(x-x')
$$
and from the uniqueness in expansion of $f(x)$ we must have
$$
\sum_n \phi_n(x)\phi_n^*(x')=\delta(x-x')
$$
That is why the last formula is the completeness condition.