- #1
- 568
- 451
- TL;DR Summary
- In QFTftGA, Lancaster and Blundell show in a (1+1) dimensional spacetime that the function ##G^+## is a Green's function for the Schrodinger equation. I need the last step of this derivation to be clarified.
Here is the conclusion of the derivation in question:
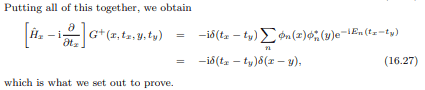
where ##\phi_n## are eigenfunctions of the Hamiltonian.
I don't see how at the very end the ##\sum ...## becomes ##\delta (x-y)##. What do I miss?
where ##\phi_n## are eigenfunctions of the Hamiltonian.
I don't see how at the very end the ##\sum ...## becomes ##\delta (x-y)##. What do I miss?