Completion of the proof of the Cosine Rule

[Prove It]

Hello my friends,

I posted this picture as a proof of the Cosine Rule in another thread,

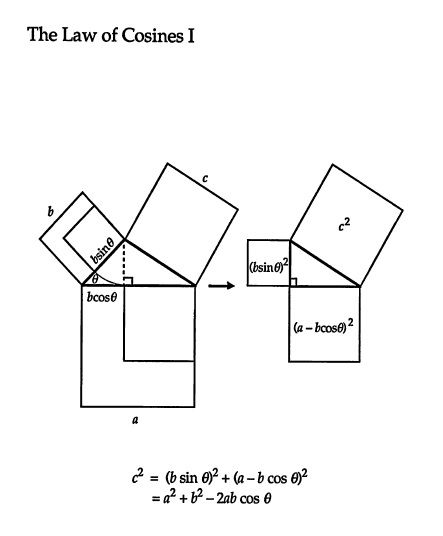
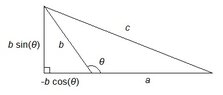
however after having a closer look at it, I believe it is incomplete. It works by drawing a segment from one of the vertices so that this segment is perpendicular to one side of the triangle, and then applying Pythagoras' Theorem.

However, if you have an obtuse-angled triangle, it is impossible to draw a segment from one of the acute vertices to make a right-angle triangle. So how is it possible to prove this relationship:

[math]\displaystyle c^2 = a^2 + b^2 - 2\,a\,b\cos{(C)}[/math]

when C is an obtuse angle?

 

[MarkFL]

Please refer to the following diagram:

View attachment 867

Note: I have used $$\sin(\pi-\theta)=\sin(\theta)$$ and $$\cos(\pi-\theta)=-\cos(\theta)$$.

By Pythagoras, we now have:

$$(a-b\cos(\theta))^2+(b\sin(\theta))^2=c^2$$

$$c^2=a^2-2ab\cos(\theta)+b^2\cos^2(\theta)+b^2\sin^2(\theta)$$

$$c^2=a^2+b^2-2ab\cos(\theta)$$