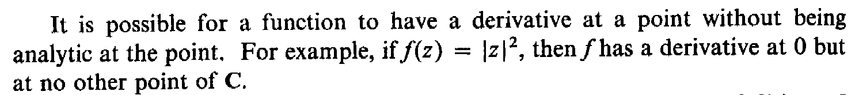Complex Derivative .... Remark in Apostol, Section 16.1 .... ....

[Math Amateur]

I am reading Tom M Apostol's book "Mathematical Analysis" (Second Edition) ...

I am focused on Chapter 16: Cauchy's Theorem and the Residue Calculus ...

I need help in order to fully understand a remark of Apostol in Section 16.1 ...

The particular remark reads as follows:

View attachment 9279Could someone please demonstrate (in some detail) how it is the case that the complex function $$f$$ has a derivative at $$0$$ but at no other point of $$\mathbb{C}$$ ... ...Help will be much appreciated ...

Peter

 

[castor28]

Hi Peter,

With $z=x+iy$, you have $f(z)=u + iv$, with $u=x^2+y^2$ and $v=0$.

What do the Cauchy-Riemann equations tell you ?

 

[Math Amateur]

Hi Peter,

With $z=x+iy$, you have $f(z)=u + iv$, with $u=x^2+y^2$ and $v=0$.

What do the Cauchy-Riemann equations tell you ?

Oh! Indeed ... Cauchy-Riemann equations are only satisfied at (0,0) ... therefore the only possible point where the derivative of f can exist is (0,0) ... and, given that the functions u and v ere continuous and have continuous first-order partial derivatives then f has a derivative at (0,0) ...

Thanks fir the help ... it is much appreciated ...

Peter