Discussion Overview
The discussion revolves around the concept of contour integration in complex analysis, specifically focusing on integrating along different shapes such as circles and squares. Participants explore the methods and implications of contour integration, including its application to infinite series and the need for parametrization. The conversation also touches on the challenges of converting integrals from real intervals to closed contours.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
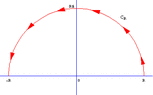
- Some participants describe contour integration as integrating along a curve rather than the real axis, requiring parametrization.
- There are various common shapes for contour integration, including circles, squares, and semi-circles.
- One participant questions how to convert an integral from $-\infty$ to $+\infty$ to a closed circular contour.
- Another participant explains that integrating along a closed curve can yield a finite value, with the integral along the diameter equating to the integral along the whole curve.
- There is a discussion about the necessity of the curved part of the contour when the diameter already spans from $-\infty$ to $\infty$.
- Some participants express interest in learning more about complex analysis and contour integration, indicating a desire for foundational knowledge.
- There are inquiries about parametrizing curves and the relationship between complex numbers and contour integration.
- Participants discuss the concept of residues and how they relate to evaluating integrals along contours.
Areas of Agreement / Disagreement
The discussion contains multiple competing views and remains unresolved regarding the necessity of the curved part of the contour and the conversion of integrals from real intervals to closed contours. Participants express varying levels of understanding and interest in the foundational concepts of complex analysis.
Contextual Notes
Participants highlight the need for a solid understanding of complex analysis concepts such as residues, parametrization, and the Cauchy integral formula, which may not be fully established in the discussion.
Who May Find This Useful
This discussion may be useful for students and enthusiasts of complex analysis, particularly those interested in contour integration and its applications in evaluating integrals and series.