Concept of 'encirclement' in Nyquist plot

[cnh1995]

I know the procedure to construct Nyquist plot and check the stability of the given system. But I am a bit confused about the concept of encirclement in the argument principle.
Consider the following figure.

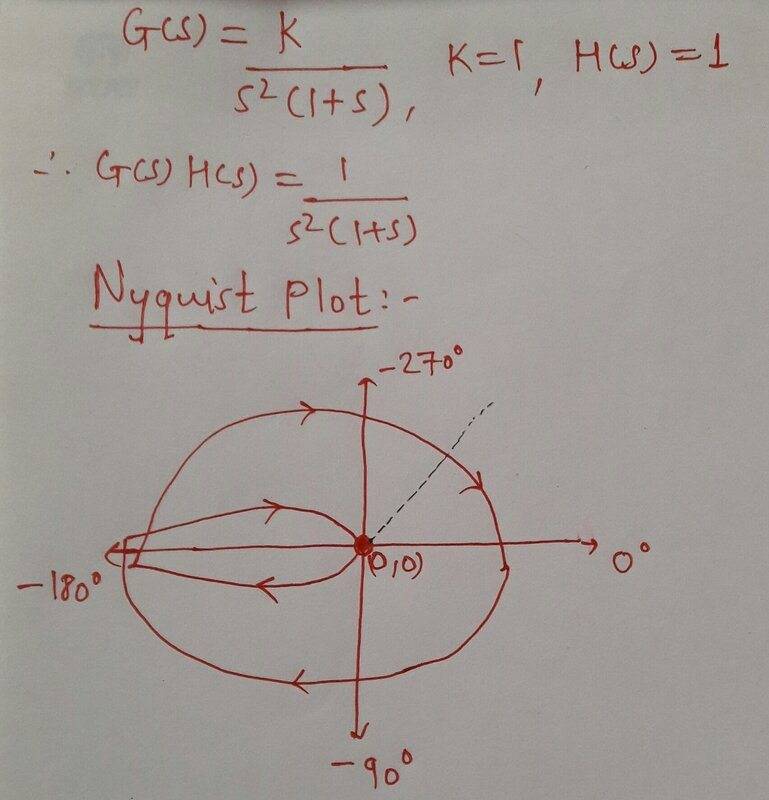
This is the Nyquist plot for the given open loop transfer function.
The Nyquist contour here is the jw axis (skipping poles at origin) and the entire RHP.
Now, as per the argument principle,
since no poles and zeros of G(s)H(s) lie in the region encircled by the Nyquist contour, the net encirclement around the origin in the Nyquist plot should also be 0.
But the origin appears to be encircled once in CW direction (dotted black line).
How can I conclude from the above plot that the net encirclement around origin is zero?
Am I missing something fundamental? (most likely).

Note: I can see the point -1+j0 is encircled twice in CW direction. So N= -2, P=0 which means CLTF poles z= P-N=2 and the closed loop system is unstable.

My confusion is about the encirclement around the origin based on the argument principle as stated earlier.

Any help is appreciated. Thanks in advance!

 

[alan123hk]

I think the detailed Nyquist plot is as follows : -

Since the contour line encircles the origin in counterclockwise direction once, and again in clockwise direction, the total number of times encircling the origin is equal to zero.