Condition for a function to be injective

[dpa]

Homework Statement

Do all the preimages on X need to have a (and of course I know only one but) image in Y for the f:x->y to be injective?
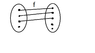
IS THE FOLLOWING FUNCTION INJECTIVE SINCE ONE ELEMENT OF FIRST DOES NOT HAVE ANY IMAGE

Homework Equations

The Attempt at a Solution

Thank You.

 

[HallsofIvy]

The way you have shown it, f is not a function from X to Y.

 

[dpa]

Thank you.